Matematik

Parabel's skæring med x-akse

22. februar 2020 af KirstineMG - Niveau: A-niveau

Hej kloge hoveder,

Jeg har en funktion f(x)=17*cos(0.0628*x). Jeg skal ved beregning finde skæringerne med x-aksen, som jeg ved der er 2 af. Min umiddelbare tanke var, at finde diskriminanten, men det kan jeg ikke finde ud af ved en sådan funktion :(.

Vedhæftet fil: Anmærkning 2020-02-22 142109.png

Brugbart svar (0)

Svar #1
22. februar 2020 af Soeffi

Brugbart svar (1)

Svar #2
22. februar 2020 af AMelev

Der er ikke tale om en parabel og derfor heller ikke en diskriminant. f er en trigonometrisk funtion.

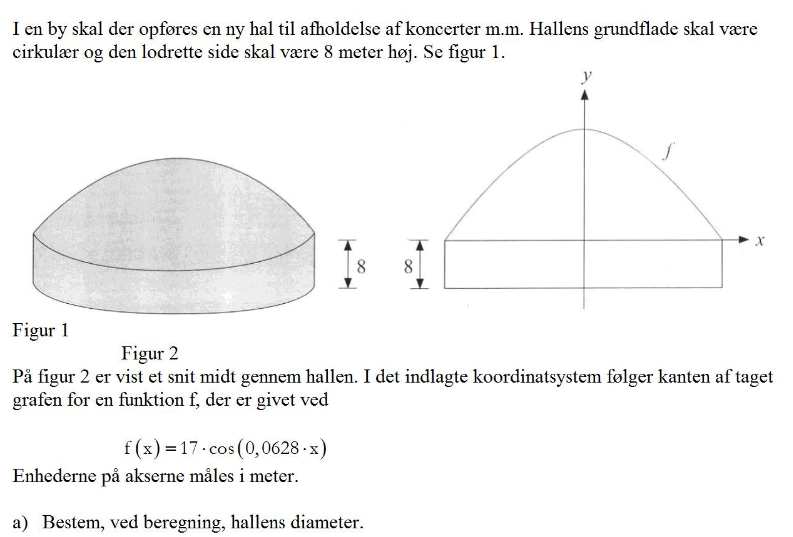
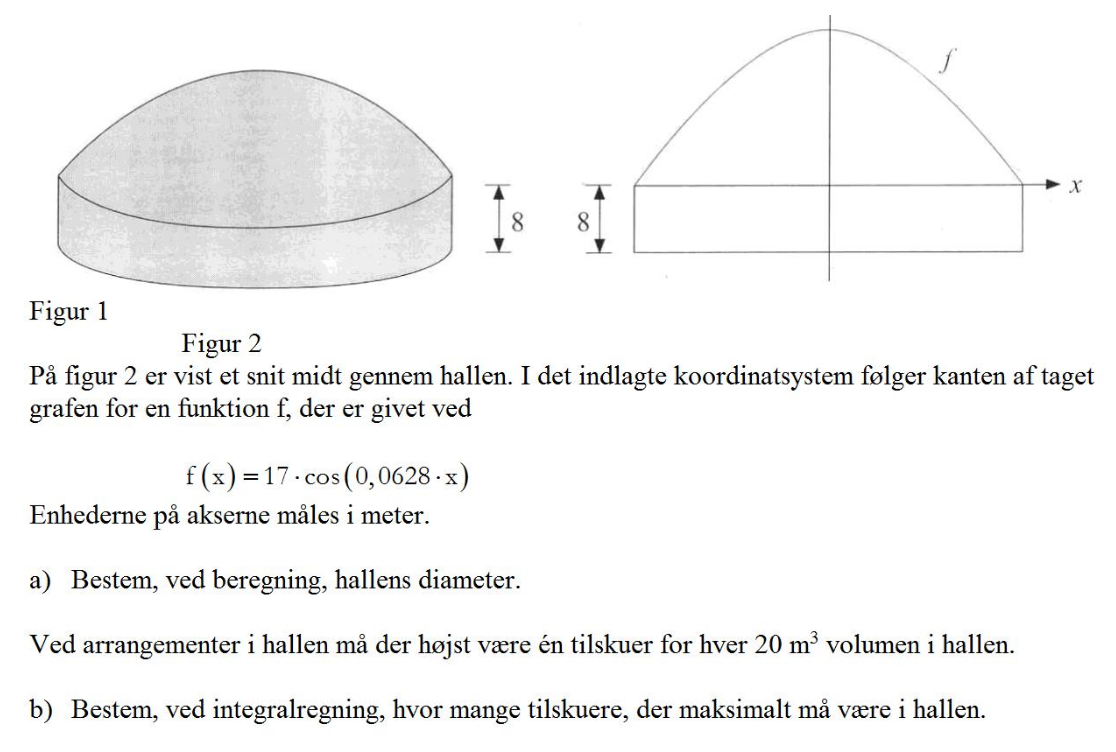
a) Hallens diameter er afstanden mellem to nabonulpunkter.
Benyt dit CAS-værktøj til at løse ligningen f(x) = 0. Det letteste er nok at løse ligningen grafisk, idet du der nemt kan finde to nulpunkter umiddelbart på hver sin side af y-aksen.
Husk at vælge Radian.

Brugbart svar (0)

Svar #3
22. februar 2020 af StoreNord

#0
Der står i opgaven, at du skal bestemme diameteren ved beregning.

Løs ligningen: 17 cos(0,0628) = 8

Brugbart svar (0)

Svar #4
22. februar 2020 af AMelev

Ad #3 Ja, det var noget vrøvl, jeg skrev i #2, sorry. Du skal løse ligningen 17·cos(0,0628x) = 8 og bestemme afstanden mellem to "naboløsninger".

Brugbart svar (0)

Svar #5
22. februar 2020 af ringstedLC

#3 og #4: Ups!

Vedhæftet fil:__0.png

Svar #6
22. februar 2020 af KirstineMG

Tak for svar,

Er det mig der er en åndsbolle for ikke at kunne se, hvorfor det er f(x)=8? Når man kigger på figur 2 på billedet vil x aksen jo være den øverste vandrette linje, så er f(x)=0 ikke rigtig nok?

Brugbart svar (0)

Svar #7
23. februar 2020 af StoreNord

Jo. #5 har ret.

Brugbart svar (0)

Svar #8
23. februar 2020 af ringstedLC

#6: Det er selvfølgelig f(x) = 0. Man ønsker, at taget skal være en halvperiode af sinusfunktionen.

Brugbart svar (0)

Svar #9
23. februar 2020 af mathon

$\small \begin{array}{lllll} &f(x)=17\cdot \cos\left ( \frac{2\pi }{100}\cdot x \right )=17\cdot \cos\left ( \frac{2\pi }{100}\cdot \left ( x+\Delta x \right ) \right )=17\cdot \cos\left (\frac{2\pi }{100}\cdot x+\frac{2\pi }{100}\cdot \Delta x \right )\\\textup{og}\\&\frac{2\pi }{100}\cdot \Delta x=p\cdot \pi \\\\&\Delta x=50\\\\\textup{nulpunkter:}&\frac{2\pi }{100}\cdot x=-\frac{\pi }{2}\\\\&x=-25\\\textup{og}\\&x=-25+\Delta x=-25+50=25\\\\\\\textup{cirkeldiameter:}&d=25-(-25)=50 \end{array}$

Svar #10
23. februar 2020 af KirstineMG

Super, det var også hvad jeg havde fået afstanden og punkterne til.
Tak for hjælpen alle sammen!

Brugbart svar (0)

Svar #11
01. marts 2020 af ringstedLC

fortsat fra: https://www.studieportalen.dk/forums/thread.aspx?id=1940835

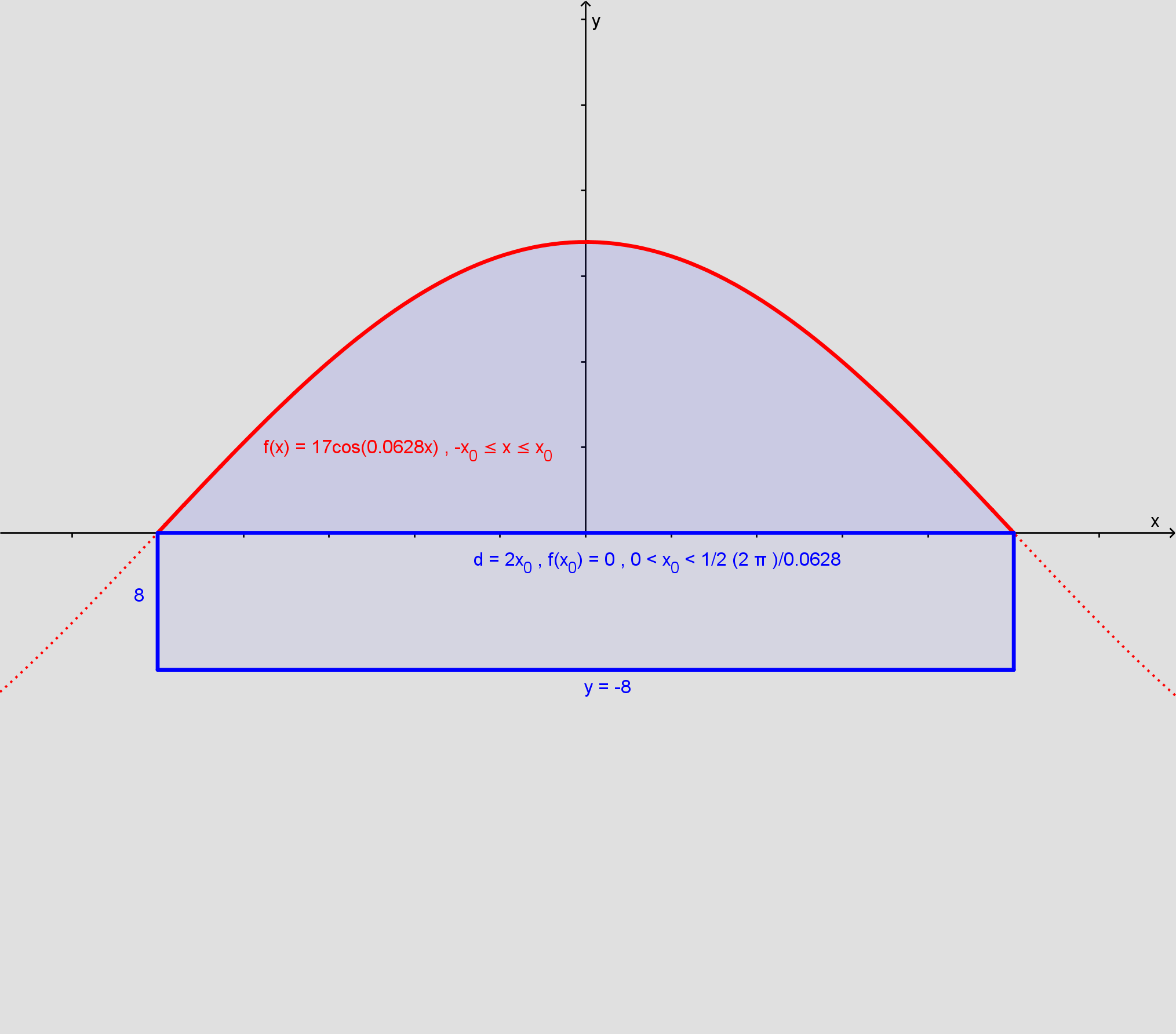
Jeg har tidligere spurgt om hjælp til denne opgave (til a delen) hvor jeg fandt at diameteren på hallen var 50, altså 25 til hver side af y-aksen, og nu spørger jeg så til b delen.

Jeg kan ikke se hvordan jeg skal bruge integralregning til at løse opgaven, snarere end bare at finde det fulde volumen og dividere med 20 (se vedhæftet).

Håber i kan hjælpe :)

Jeg bruger Maple som CAS-værktøj, hvis det kan hjælpe

Jeg har kun kendskab til nedenstående metode, hvor der bruges integralregning. Hvis du kender en anden metode, vil jeg gerne se den.

Et simpelt legemes volume, fx en cylinder:

$\begin{align*} V_{Cyl.} &= \pi \,r^2h \\ &= \pi \cdot 1^2\cdot 4=4\,\pi \end{align*}$

Når cylinderen indtegnes i koordinatsystemet (2D), kan dens volume ligeledes beregnes ved:

$\begin{align*} h=4&=f(x)\;,\;0\leq x\leq 1=r \\ V_{Cyl.} &= 2\,\pi \int_{0}^{r}x\cdot f(x)\,dx \\ &= 2\,\pi \int_{0}^{1}x\cdot 4\,dx \\ &= 2\,\pi \left [2x^2\right ]_{0}^{1} \\ &= 2\,\pi \left (2-0\right )=4\,\pi \end{align*}$

$\begin{align*} V &= V_{Cyl.}+V_{Kuppel} \\ &= \pi \,r^2h+2\,\pi \int_{a}^{b}x\cdot f(x)\,dx \\ f(x) &= 0\Rightarrow b=\tfrac{1250}{157}\,\pi\approx25\;,\;b>0 \\V &= \pi \cdot \left (\tfrac{1250}{157}\,\pi\right )^2\cdot 8+2\,\pi\int_{0}^{\,\tfrac{1250}{157}\,\pi}x\cdot f(x)\,dx \\ V &\approx 15723\text{ m}^3+15459\text{ m}^3= 31182 \text{ m}^3 \\ \text{Maksimalt antal tilskuere} &= \tfrac{V}{20}\approx\;? \end{align*}$

En detalje: Ved beregning med eksakt værdi af b og r, kan der faktisk være én tilskuer mere end ved b = r = 25.

Brugbart svar (0)

Svar #12
02. marts 2020 af mathon

Volumen i oversigt:

.
$\small \begin{array}{lllr}\textup{Volumen under tag:}&V_{tag}=2\pi \cdot \int_{0}^{25}x\cdot 17\cdot \cos\left ( \frac{\pi }{50}\cdot x \right )\, \mathrm{d}x&=&15443.7\\\\\textup{Volumen af cylinder:}&V_{hyl}=8\cdot \pi \cdot 25^2&=&\underline{15708.0}\\\\\textup{Sum:}&&&31151.7\\\\\\\textup{Maksimalt antal personer:}&\frac{31151.7\; m^3}{20\; \frac{m^3}{pers}}&=&1558\; pers. \end{array}$

Brugbart svar (0)

Svar #13
03. marts 2020 af mathon

hvort jeg har tilladt mig at erstatte 0.0628 med $\small \tfrac{2\pi }{100}=\tfrac{\pi }{50}$

Skriv et svar til: Parabel's skæring med x-akse

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.