Matematik
Optimering af cylinder
Jeg har en kegleform med en cylinderformet kabine inden i. Alle mål er i meter.
Jeg skal vælge radius r og højden h, således at kabinenes rumfang V bliver størst muligt.
Hvordan gør jeg dette?
Har adgang til maple, og geogebra.
Svar #2
24. februar 2020 af Soeffi
#1. Rumfanget af cylinderen er: π·r2·h. Der er en sammenhæng mellem r og h, som kan skrives som en lineær funktion: h = (-5/3)·r + 5. Dette giver at rumfanget udtrykt ved radius er:
V(r) = π·r2·((-5/3)·r + 5) = 5·π·r2·(1 - r/3).
Maksimum findes ved at differentiere og sætte lig med 0: 5·π·r2·(1 - r/3).
V'(r) = −5·π·r·(r - 2). V'(r) = 0 ⇒ r = 0 eller r = 2. Ved at lave en fortegnsundersøgelse for V'(r) kan man vise, at r = 2 giver et maksimum.
Svar #3
29. marts 2023 af fuckmath
#2#1. Rumfanget af cylinderen er: π·r2·h. Der er en sammenhæng mellem r og h, som kan skrives som en lineær funktion: h = (-5/3)·r + 5. Dette giver at rumfanget udtrykt ved radius er:
V(r) = π·r2·((-5/3)·r + 5) = 5·π·r2·(1 - r/3).
Maksimum findes ved at differentiere og sætte lig med 0: 5·π·r2·(1 - r/3).
V'(r) = −5·π·r·(r - 2). V'(r) = 0 ⇒ r = 0 eller r = 2. Ved at lave en fortegnsundersøgelse for V'(r) kan man vise, at r = 2 giver et maksimum.
jeg har også fået denne opgave, men jeg forstår ikke hvor (-5/3)*r+5 kommer fra
Svar #4
29. marts 2023 af M2023
#3 jeg har også fået denne opgave, men jeg forstår ikke hvor (-5/3)*r+5 kommer fra
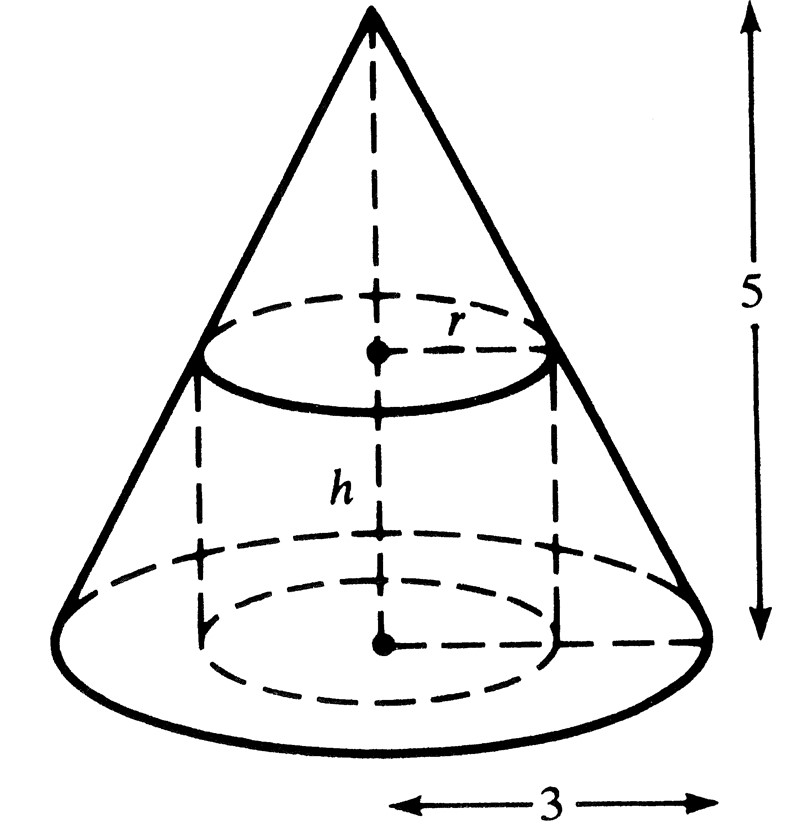
På tegningen er der to retvinklede trekanter, der er ligedannede. Den ene har kateterne 3 og 5, mens den anden har kateterne r (kort side) og 5 - h (lang side). Eftersom de to trekanter er ligedannede, så gælder, at
5/3 = (5 - h)/r ⇔ (5/3)·r = 5 - h ⇔ h = 5 - (5/3)·r.
Svar #5
30. marts 2023 af fuckmath
#4#3 jeg har også fået denne opgave, men jeg forstår ikke hvor (-5/3)*r+5 kommer fra
På tegningen er der to retvinklede trekanter, der er ligedannede. Den ene har kateterne 3 og 5, mens den anden har kateterne r (kort side) og 5 - h (lang side). Eftersom de to trekanter er ligedannede, så gælder, at
5/3 = (5 - h)/r ⇔ (5/3)·r = 5 - h ⇔ h = 5 - (5/3)·r.
V(r) = π·r^2·((-5/3)·r + 5) = 5·π·r^2·(1 - r/3)
hvordan kommer man så frem til (1 - r / 3)
Svar #6
30. marts 2023 af M2023
#5.
#4#3 jeg har også fået denne opgave, men jeg forstår ikke hvor (-5/3)*r+5 kommer fra
På tegningen er der to retvinklede trekanter, der er ligedannede. Den ene har kateterne 3 og 5, mens den anden har kateterne r (kort side) og 5 - h (lang side). Eftersom de to trekanter er ligedannede, så gælder, at
5/3 = (5 - h)/r ⇔ (5/3)·r = 5 - h ⇔
h = 5 - (5/3)·r = 5 - 5·(r/3) = 5·(1 - r/3).
Skriv et svar til: Optimering af cylinder
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.



