Matematik

Differentialregning

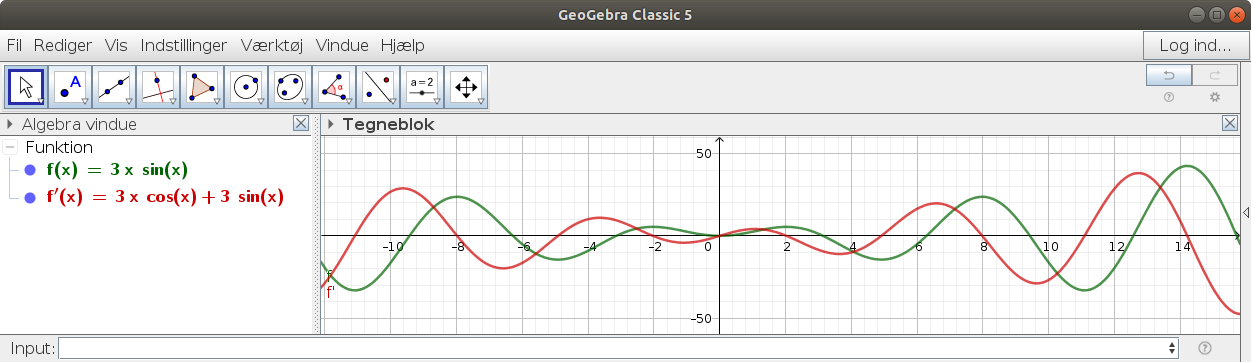
27. marts 2020 af MGjosefine - Niveau: B-niveau

Jeg skal differentiere

f(x)=3x*sin(x)

f(x)=In (3x-5)

- en der måske vil hjælpe / tak på forhånd

Brugbart svar (0)

Svar #1
27. marts 2020 af StoreNord

f(x) er en produktfunktion.

https://www.webmatematik.dk/lektioner/matematik-b/differentialregning/regneregler-for-differentialkvotienter

Brugbart svar (0)

Svar #2
27. marts 2020 af StoreNord

Vedhæftet fil:Skærmbillede fra 2020-03-27 20-21-40.png

Svar #3
27. marts 2020 af MGjosefine

Jeg er stadigvæk ikke helt sikker på hvordan man laver f(x)=ln(3x-5)

Brugbart svar (0)

Svar #4
27. marts 2020 af Anders521

# 3 Giv funktionen et andet navn f.eks. g. Med g(x) = ln(3x-5), hvor x>3/5 har du en sammensat funktion hvor den ydre har regneforskriften ln(x) og den indre 3x-5.

Brugbart svar (0)

Svar #5
27. marts 2020 af Mathias7878

Funktionen

$f(x) = \ln(3x-5)$

er en sammenfunktion på formen

$f(x) = h(g(x))$

hvor

$h(x) = \ln(x) \ \text{og} \ g(x) = 3x-5$

hvilket vil sige, at du skal bruge kædereglen for at differentiere udtrykket. Kædereglen siger, at

$f'(x) = h'(g(x)) \cdot g'(x)$

og med ord betyder det, at du skal differentiere den ydre funktion og lade den indre være uberørt og gange med indre differentieret.

- - -

Brugbart svar (0)

Svar #6
28. marts 2020 af mathon

eller noteret:
$\small \frac{\mathrm{d} f}{\mathrm{d} x}=\frac{\mathrm{d} f}{\mathrm{d} y}\cdot \frac{\mathrm{d} y}{\mathrm{d} x}$
$\small f(y)=\ln(y)\qquad \frac{\mathrm{d} f}{\mathrm{d} y}=\frac{1}{y}\quad y>0$

$\small y=3x-5\qquad \frac{\mathrm{d} y}{\mathrm{d} x}=3\quad\;\;\, \, x>\frac{5}{3}$

$\small f{\, }'(x)=\frac{\mathrm{d} f}{\mathrm{d} x}=\frac{1}{y}\cdot 3=\frac{3}{y}=\frac{3}{3x-5}$

Skriv et svar til: Differentialregning

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.