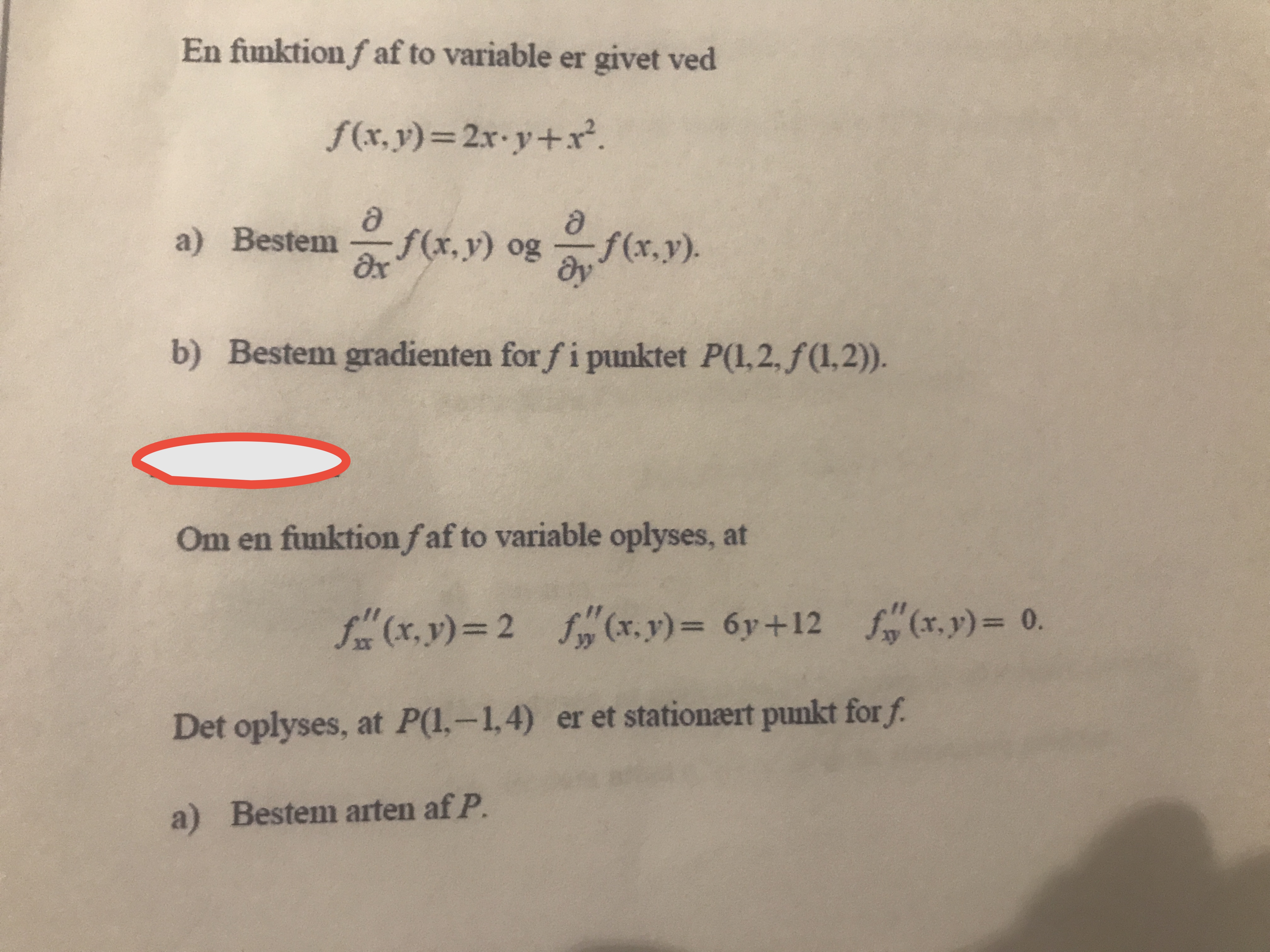Matematik

!!!

01. april 2020 af smisch - Niveau: A-niveau

Jeg kan simpelthen ikke komme videre.. sidder fast ved de opgaver jeg har vedhæftet. Håber der er nogen som kan hjælpe.

Vedhæftet fil: ny opg..JPG

Brugbart svar (0)

Svar #1
01. april 2020 af mathon

Brugbart svar (0)

Svar #2
01. april 2020 af Moderatoren

Se evt. hjælpen her:

https://www.studieportalen.dk/forums/thread.aspx?id=1949390#1949429

Og skriv så, hvor du præcist sidder fast.

Og:

Giv dit indlæg en sigende titel. På den måde er der større sandsynlighed for, at lektiehjælperne kan finde dit spørgsmål.

Brugbart svar (1)

Svar #3
01. april 2020 af mathon

$\small \begin{array}{lllllll}a)&&f(x,y)=2\cdot x\cdot y+x^2\\\\&&\frac{\partial }{\partial x}(f(x,y))=2y+2x\\\\&&\frac{\partial }{\partial y}(f(x,y))=2x\\\\\\b)&\textup{gradienten i:}&P(1,2,f(1,2))=(1,2,5)\\\\&&\textup{er:}\quad \begin{pmatrix} 2\cdot 1+2\cdot 2\\2\cdot 1 \end{pmatrix}=\begin{pmatrix} 6\\2 \end{pmatrix} \end{array}$

Svar #4
01. april 2020 af smisch

Mange tak for hjælpen

Brugbart svar (1)

Svar #5
01. april 2020 af mathon

$\small \small \begin{array}{lllllll}a)&&f_{yy}{\,}''(1,-1)=6\cdot (-1)+12=6\\\\&&f_{xx}{\,}''(1,-1)\cdot f_{yy}{\,}''(1,-1)-\left (f_{xy}{\,}''(1,-1) \right )^2=2\cdot 6-0=6>0\\\\&\textup{da}&f_{xx}{\,}''(1,-1)>0\textup{ og }f_{xx}{\,}''(1,-1)\cdot f_{yy}{\,}''(1,-1)-\left (f_{xy}{\,}''(1,-1) \right )^2>0\textup{ er}\\\\&&P(1,-1,4)\textup{ et lokalt minimumspunkt.} \end{array}$

Svar #6
01. april 2020 af smisch

Tusind tak :)

Brugbart svar (0)

Svar #7
01. april 2020 af AMelev

Væn dig til at bruge Formelsamlingen, som der er linket til i din anden tråd med lignende problemstilling.

Skriv et svar til: !!!

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.