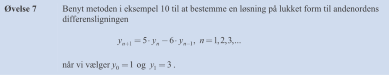Andenordensdifferensligning

Du skal nok starte med at forstå eksempel 10. Hvad forstår du ikke?

#0.

Forstår ikke hvor tallene kommer fra eller hvad jeg skal gøre, vil bare gerne have en skal gøre det for mig skridt for skridt med lidt forklarende tekst

Hvad går eksempel 10 ud på? Ka' du sende et billede af det?

#5.

#2.

Man har følgende (homogene) andenordens differensligning: y_n+1 = 5·y_n - 6·y_n-1. 

Leddene samles på venstre side: y_n+1 + (-5)·y_n + 6·y_n-1 = 0

Man betragter den tilsvarende andengradsligning: 1·x² + (-5)·x + 6 = 0

Denne har diskriminanten: 25 - 4·1·6 = 1

Rødderne er: x = 5/2 ± 1/2 ⇒ x₁ = 2 og x₂ = 3

I følge eksempel 10, så giver det den lukkede løsning: y_n = c₁·2ⁿ + c₂·3ⁿ

C₁ og C₂ findes ud fra y₀ og y₁:

y₀ = 1 ⇒ c₁·2⁰ + c₂·3⁰ = 1 ⇒ c₁ + c₂ = 1 ⇒ c₂ = 1 - c₁

y₁ = 3 ⇒ c₁·2¹ + c₂·3¹ = 3 ⇒ c₁·2 + c₂·3 = 3 ⇒ c₁·2 + (1 - c₁)·3 = 3 ⇒ -c₁ + 3 = 3 ⇒ c₁ = 0  

Hvilket giver: c₁ = 0 og c₂ = 1 og dermed: y_n = 3ⁿ