Matematik

Stamfunktion

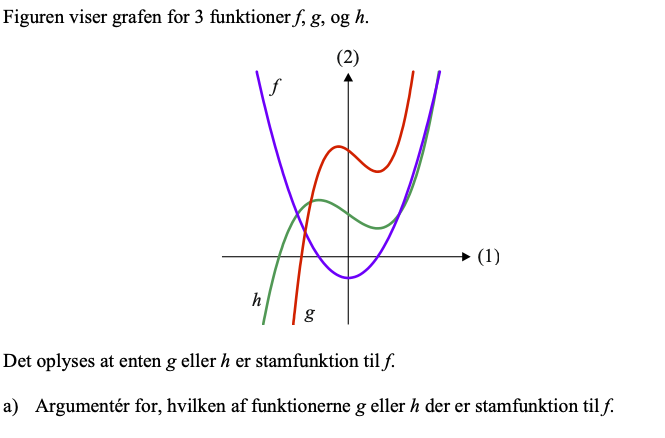
23. maj 2020 af MARIOO123 - Niveau: A-niveau

Hvordan vil jeg udfra skitserne oplyse hvilken graf der er stamfunktionen til f?

Vedhæftet fil: Skærmbillede 2020-05-23 kl. 14.44.51.png

Brugbart svar (0)

Svar #1
23. maj 2020 af peter lind

Brugbart svar (1)

Svar #2
23. maj 2020 af peter lind

Brug at for for f(x) = 0 er der enten minimum eller maksimum f for dens stamfunktion

Svar #3
23. maj 2020 af MARIOO123

Så må det være grafen h der er stamfunktionen til f, idet i f(x)=0 så har stamfunktionen (grafen h) sin lokale maksimum og lokale minimum.

Brugbart svar (0)

Svar #4
23. maj 2020 af ringstedLC

#3: Argument₁: Ekstrema for h og rødder for f er sammenfaldende:

$\begin{align*} f(x)=0&\Rightarrow x=\left\{\begin{matrix}x_1\\x_2\\ \end{matrix}\right. \\ \left (g(x)=\int f(x)\dx \wedge h(x)\neq \int f(x)\,dx \right ) &\vee \left (g(x)\neq \int f(x)\dx \wedge h(x)= \int f(x)\,dx \right ) \\ \underbrace{g'(x)=f(x)} \qquad \qquad \wedge \qquad \underbrace{h'(x)\neq f(x)}\qquad & \vee \qquad \underbrace{g'(x)\neq f(x)} \qquad \wedge \qquad \underbrace{h'(x)=f(x)} \\ \underbrace{\Bigl (g'(x_1)=g'(x_2)=0 \Bigr ) \wedge \Bigl (h'(x_1)\neq 0 \vee h'(x_2)\neq 0 \Bigr )} & \vee \underbrace{\Bigl (g'(x_1)\neq 0 \vee g'(x_2)\neq 0\Bigr) \wedge \Bigl (h'(x_1)=h'(x_2)=0\Bigr)} \\ falsk \qquad \qquad \qquad \qquad \qquad & \qquad \qquad \qquad \qquad \qquad \quad sand \\ \Rightarrow h'(x_1)=h(x_2)=f(x_1)=f(x_2) &\Rightarrow h(x)=\int f(x)\,dx \end{align*}$

Argument₂: Hældning for h og funktionsværdi af f er sammenfaldende:

$\begin{align*} f(x)=0&\Rightarrow x=\left\{\begin{matrix}x_1\\x_2\\ \end{matrix}\right. \\ \left.\begin{matrix} f(x)>0\;,\;-\infty<x<x_1 \Rightarrow \left\{\begin{matrix} h\text{ tiltager}\quad\\ g\text{ tiltager}\quad \end{matrix}\right. \\\\ f(x)<0\;,\quad x_1<x<x_2 \Rightarrow \left\{\begin{matrix} h\text{ aftager}\\ g\text{ tilt./aft.} \end{matrix}\right. \\\\ f(x)>0\;,\;\;x_2<x<\infty \Rightarrow \left\{\begin{matrix} h\text{ tiltager}\\ g\text{ tiltager} \end{matrix}\right. \\ \end{matrix}\right\} &\Rightarrow h(x)=\int f(x)\,dx \end{align*}$

Brugbart svar (0)

Svar #5
27. februar kl. 01:19 af ringstedLC

#4 "Opfriskes!

Argument₁: Ekstrema for h og rødder for f er sammenfaldende. Dette gælder ikke for g:

$\begin{align*} f(x)=0 &\Rightarrow x=\left\{\begin{matrix}x_1\\x_2\\ \end{matrix}\right. \\ \Biggl(g(x)=\int\!f(x)\,\mathrm{d}x \;\, \wedge \qquad\quad\;\, h(x)\neq \int\!f(x)\,\mathrm{d}x \Biggr) \; &\vee \qquad\;\;\; \Biggl(g(x)\neq \int\!f(x)\,\mathrm{d}x \;\; \wedge \qquad\;\; h(x)=\int\!f(x)\,\mathrm{d}x \Biggr) \\ \Bigl(g\,'(x)=f(x) \qquad\;\;\, \wedge \qquad\quad\, h'(x)\neq f(x) \Bigr) \qquad\;\;\; &\vee \qquad\;\, \Bigl(g\,'(x)\neq f(x) \qquad\quad \wedge \qquad\; h'(x)=f(x)\Bigr) \\ \underset{\textup{falsk }}{\underbrace{{\color{Red} g\,'(x_1)=0} \wedge g\,'(x_2)=0 \; \wedge \; \Bigl(\,{\color{Red} h'(x_1)\neq 0} \vee h'(x_2)\neq 0\,\Bigr)}} \; &\vee \; \underset{\textup{sand }}{\underbrace{\Bigl(g\,'(x_1)\neq 0 \vee g\,'(x_2)\neq 0\Bigr) \wedge \; h'(x_1)=0 \wedge h'(x_2)=0}} \\ h'(x_1)=h'(x_2)=f(x_1)=f(x_2)=0 \quad &\Rightarrow \quad h(x)=\int\!f(x)\,\mathrm{d}x \end{align*}$

Argument₂: Hældning for h og funktionsværdi af f er sammenfaldende. Dette gælder ikke for hældningen af g og funktionsværdien af f :

Skriv et svar til: Stamfunktion

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.