Matematik

Vektorfunktioner

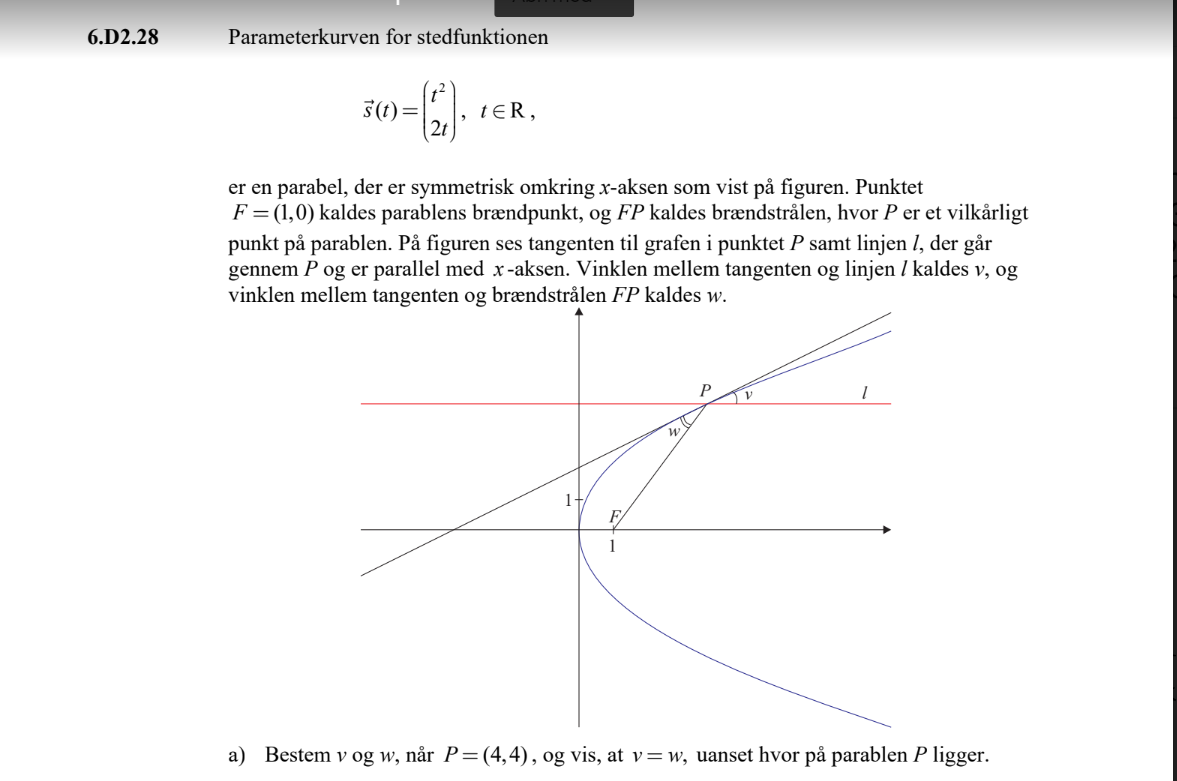
24. maj 2020 af Matmatmatma - Niveau: A-niveau

Hej

Jeg kunne godt bruge et hint til at vise, at v=w uanset koordinatsættet for P.

Vedhæftet fil: Udklip11.PNG

Brugbart svar (0)

Svar #1
24. maj 2020 af peter lind

Brugbart svar (0)

Svar #2
24. maj 2020 af peter lind

Jeg går ud fra at du har gennemført beregnigerne for P = (4, 4) Gennemfør de samme beregninger med

P = (t², 2t)

Brugbart svar (0)

Svar #3
24. maj 2020 af mathon

Brugbart svar (0)

Svar #4
24. maj 2020 af ringstedLC

#0: Q er skæringen mellem tangenten og x-aksen. Vis at |FP| og |FQ| udtrykt ved t er den samme. Da er ΔFPQ ligebenet og da vinkel Q = v, må det gælde, at v = w.

Brugbart svar (0)

Svar #5
24. maj 2020 af mathon

$\small \begin{array}{llllll} & \overrightarrow{s}(t)=\begin{pmatrix}t^2\\2t \end{pmatrix}\\\\& \overrightarrow{s}{\,}'(t)=\begin{pmatrix}2t\\2 \end{pmatrix}\\\\& \overrightarrow{FP}=\begin{pmatrix}t^2-1\\2t \end{pmatrix}\\\\& \cos(w)=\frac{\begin{pmatrix}t^2-1\\2t \end{pmatrix}\cdot \begin{pmatrix}2t \\ 2 \end{pmatrix}}{\sqrt{(t^2-1)^2+(2t)^2}\cdot \sqrt{(2t)^2+2^2}}=\frac{2t(t^2+1)}{\sqrt{(t^2+1)^2 }\cdot 2 \cdot \sqrt{t^2+1}}=\frac{t}{\sqrt{t^2+1}}\\\\\\& \cos(v)=\frac{\begin{pmatrix}2t\\2 \end{pmatrix}\cdot \begin{pmatrix}1 \\ 0 \end{pmatrix}}{\sqrt{(2t)^2+2^2}\cdot 1}=\frac{2t}{2\sqrt{t^2+1}}=\frac{t}{\sqrt{t^2+1}}\\\\ \textup{dvs}&\cos(w)=\cos(v)\\ \textup{og dermed}\\& w=v \end{array}$ ?

Skriv et svar til: Vektorfunktioner

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.