Fysik

beregn erstatningsresistansen for hele koblingen

18. juni 2020 af Skuls - Niveau: B-niveau

Denne kobling kan opfattes som en blanding af serie- og parallelkoblinger

12Ω, 20Ω,10Ω,18Ω

Hvordan regner jeg det ud

Brugbart svar (0)

Svar #1
18. juni 2020 af Eksperimentalfysikeren

Hvordan er de forbundet med hinanden?

Svar #2
18. juni 2020 af Skuls

Her

Vedhæftet fil:818EBE96-D2A4-436D-B60C-F19EAAD8DE61.jpeg

Brugbart svar (0)

Svar #3
18. juni 2020 af Eksperimentalfysikeren

Du har to modstande (10Ω og 18Ω), der er parallelforbundne. Dem kan du erstatte med en enkelt modstend, hvis størrelse findes af: 1/R_p = 1/10Ω + 1/18Ω.

Når du har gjort det, har du den nye modstand i serie med de 12Ω. Dem erstatter du med en modstand hvis størrelse er summen af de to modstandes størrelser, dvs. 12Ω + R_p. Til sidst har du en parallelforbindelse af to modstande. Der bruger dusamme formel som i første tilfælde.

Svar #4
18. juni 2020 af Skuls

Jeg har lidt svært ved opgaven, men skal jeg så beregne summen af 1/10Ω + 1/18Ω, så det bliver

12Ω + 0,15

Brugbart svar (0)

Svar #5
18. juni 2020 af Soeffi

#0.

Brugbart svar (0)

Svar #6
18. juni 2020 af janhaa

$R(tot)=\frac{1}{10}+\frac{1}{18}+12+20\approx 38,4\, (\Omega)$

trur eg...

Brugbart svar (0)

Svar #7
18. juni 2020 af PeterValberg

$R_{tot}=\left((12+(10^{-1}+18^{-1})^{-1})^{-1}+20^{-1}\right)^{-1}$

- - -

mvh.

Peter Valberg
(YouTube)

Brugbart svar (0)

Svar #8
18. juni 2020 af Soeffi

#0. Prøv at finde R₃ på nedenstående billede...

Vedhæftet fil:1967150.png

Brugbart svar (0)

Svar #9
18. juni 2020 af mathon

$\small \small \small R_{\textup{total}}=\textup{sum}\left ( \left \{ \frac{10\cdot 18}{10+18},12,20 \right \} \right )$

Svar #10
18. juni 2020 af Skuls

#6
$R(tot)=\frac{1}{10}+\frac{1}{18}+12+20\approx 38,4\, (\Omega)$

trur eg...

Hvad er det resultatet for

Brugbart svar (0)

Svar #11
18. juni 2020 af PeterValberg

Den samlede/totale modstand får jeg til ca. 9,59 Ohm

- - -

mvh.

Peter Valberg
(YouTube)

Brugbart svar (0)

Svar #12
18. juni 2020 af mathon

#6 og #9 er forkerte resultater.

$\small \small \begin{array}{lllll} \textup{Skal v\ae re}&R_{\textup{total}}=\left (\left (\left (\frac{1}{10}+\frac{1}{18} \right )^{-1}+12 \right )^{-1}+20^{-1} \right )^{-1} \end{array}$

Brugbart svar (0)

Svar #13
18. juni 2020 af PeterValberg

Nej....det er rigtig nok

- - -

mvh.

Peter Valberg
(YouTube)

Brugbart svar (0)

Svar #14
18. juni 2020 af PeterValberg

Vedr # 12

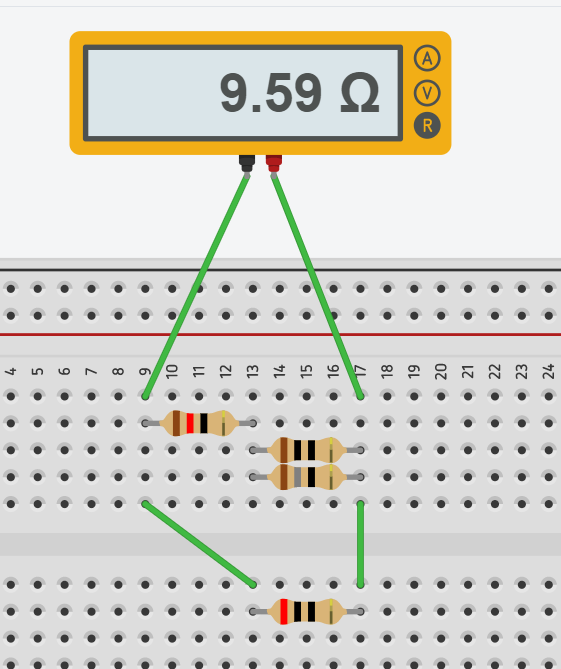
Vi er fuldstændig enige om metoden, - jeg får det bare til 9,59 Ω

hvad får du det til?

- - -

mvh.

Peter Valberg
(YouTube)

Brugbart svar (0)

Svar #15
18. juni 2020 af PeterValberg

- - -

mvh.

Peter Valberg
(YouTube)

Vedhæftet fil:Udklip.PNG

Brugbart svar (0)

Svar #16
18. juni 2020 af PeterValberg

#0 Se bort fra #13

@mathon
Jeg indser nu, at du henviser til #6 og #9 og ikke til #11
(dine henvisninger var vist ikke med første gang?)

Jeg tror roligt, at vi kan erklære os enige i metoden og resultatet.... :-)

- - -

mvh.

Peter Valberg
(YouTube)

Svar #17
18. juni 2020 af Skuls

#14
Vedr # 12

Vi er fuldstændig enige om metoden, - jeg får det bare til 9,59 Ω

hvad får du det til?

Hvordan får du det til 9,59

Brugbart svar (0)

Svar #18
18. juni 2020 af mathon

Beregn selv #12.

Brugbart svar (1)

Svar #19
18. juni 2020 af Eksperimentalfysikeren

I det følgende udelades enhederne:

R1 er parallelforbindelsen af 10 Ohm og 18Ohm: 1/R1 = 1/10 + 1/18 = 9/90 + 5/90 = 14/90 = 7/45.

R1 = 45/7 = 6,429

R2 er seriefobndelsen af 12 Ohm og R1: R2 = 12 + 6,429 = 18,429

R3 er parallelforbindelsen af 20 Ohm og R2 : 1/R3 = 1/20 + 1/18,429

Der tages den reciprokke værdi på begge sider: R3 = 20*18,429/(20+18,428) = 9,591

Dette afrundes til 2 decimaler: 9,59 Ohm, som PeterValberg også kom frem til.

Svar #20
18. juni 2020 af Skuls

Mange tak for svaret, men hvor får du 90 fra i den første linje

Forrige 1 2 Næste

Der er 21 svar til dette spørgsmål. Der vises 20 svar per side. Spørgsmålet kan besvares på den sidste side. Klik her for at gå til den sidste side.