Matematik
Areal område
Hej Alle
Jeg har brug for lift hjælp og inspiration for følgende opgave :
Vi har følgende funktion f(x) = 0.08 x2 (x fra 0 tl 10)
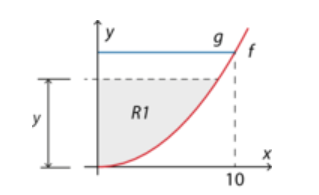
Bestem den y-værdi som vist på figuren, der giver et areal på R1 = 40.
figuren vedhæftes:
Tak på forhånd.
Svar #3
28. juni 2020 af DeepOcean
Areal R1 er ikke under grafen den er mellem y-aksen og grafen.! så jeg tro rikke den er rigtigt !
Svar #5
28. juni 2020 af StoreNord
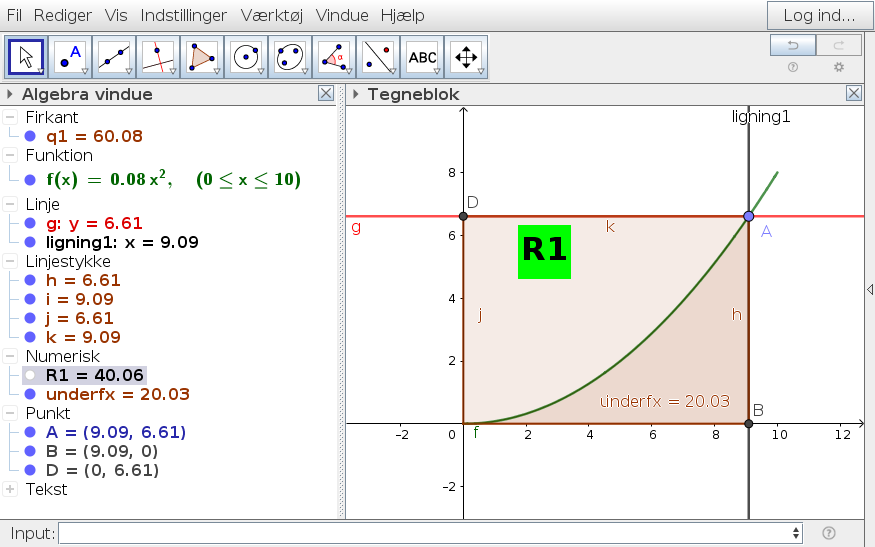
I hvert fald skulle du gerne få: y= ca 6.61 , som er den røde linje på denne tegning.
Svar #7
28. juni 2020 af DeepOcean
#5 : Du har ret med 6.61. Men hvordan kom du frem til det ? .Jeg savner beregning .
Hvordan har du fundet punkt. B ?
Svar #8
28. juni 2020 af StoreNord
A er et flytbart punkt på grafen.
Den røde linje laves med y=y(A). Den lodrette laves tilsvarende med x=x(A).
B og D er deres skæringspunkter med akserne.
Så har jeg bare flyttet A, så arealet kom til at passe. Ikke særlig matematisk.
Det var mest ment som supplement til andre metoder. Måske kunne nogen tage fejl.
Svar #9
28. juni 2020 af peter lind
#3 så kan du løse den som x2 - ∫0x0,8*t2dt = 40
#4 for y > 0 gælder det at y = 0,08*x2 <=>x2 = y/0,08 = x2 <=> x = kvrod (y/0,08)= så integranden er kvrod(y/0,08)
Skriv et svar til: Areal område
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.