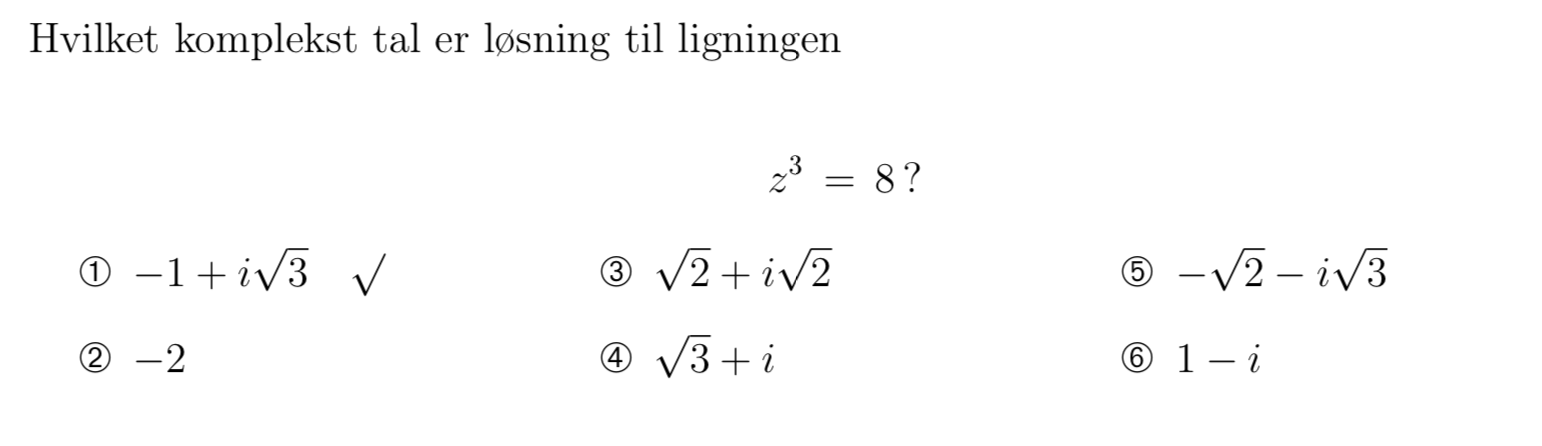Matematik

Hvilket komplekst tal er løsning til ligningen z^3=8

23. september 2020 af 123hej10 - Niveau: Universitet/Videregående

Jeg sidder med en MC prøve fra 2013 med opgaven:

Der er 6 muligheder og jeg er godt klar over at jeg i princippet kunne gå i gang med at finde den 3 rod af alle de 6 komplekse tal og se hvilket der gav 8 (de 6 muligheder vedhæftet).

Mit spørgsmål er om nogen kender en lettere metode eller en form for udelukkelsesmetode i denne opgave så jeg ikke sidder til prøven og skal finde den 3. rod af alle tallene?

Vedhæftet fil: Skærmbillede 2020-09-23 kl. 23.54.55.png

Brugbart svar (0)

Svar #1
24. september 2020 af Capion1

Vi ved, at ligningen har en reel rod, z = 2.
Drej vektoren $\binom{2}{0}$ +120º og igen +120º

Brugbart svar (0)

Svar #2
24. september 2020 af mathon

Svar #3
24. september 2020 af 123hej10

hej, så ud fra #1 så ved jeg bare at vektoren (2 0) + 120 grader og igen 120 grader, at der giver - $-1+i sqrt(3)$ . Fordi hvis det er noget jeg burde vide så har jeg et problem...

Brugbart svar (0)

Svar #4
24. september 2020 af Capion1

Den ene komplekse rod ligger i 2.kvadrant, hvor fortegnene for realdel og imaginærdel er henh.vis. - +
Den anden komplekse rod ligger i 3.kvadrant, hvor fortegnene for realdel og imaginærdel er henh.vis. - -
og hvor vektorlængden for alle tre rødder er 2.

Brugbart svar (0)

Svar #5
24. september 2020 af Capion1

Tegn en cirkel med centrum i (0 , 0) og radius 2.
Punktet (2 , 0) er den reelle løsning z = 2.
Drej punktet +120º som er næste (komplekse) løsning.
Drej yderligere punktet +120º som er sidste (komplekse) løsning.

Brugbart svar (0)

Svar #6
24. september 2020 af mathon

eventuelt
$\small \small \begin{array}{lllll} \textup{rodtjek:}\\& \begin{array}{lllll} \left (-1+\textbf{\textit{i}}\cdot \sqrt{3} \right )^3=&(-1)^3+3\cdot (-1)^2\cdot\left ( \textbf{\textit{i}}\cdot \sqrt{3} \right )+ 3\cdot (-1)\cdot\left ( \textbf{\textit{i}}\cdot \sqrt{3} \right )^2+\left (\textbf{\textit{i}}\cdot \sqrt{3} \right )^3=\\\\& -1+\textbf{\textit{i}}\cdot 3\sqrt{3}+9-\textbf{\textit{i}}\cdot 3\sqrt{3}=8 \end{array} \end{array}$

Brugbart svar (0)

Svar #7
24. september 2020 af Soeffi

#2.

Der er to måder: løs ligningen z³ = 8 ved hjælp af standardformlen eller prøv dig frem ved at sætte løsningsforslagene i tredje. Det første giver:

$z^n =r\cdot e^{i\cdot v}\Leftrightarrow z=\sqrt[n]{r}\cdot e^{i\cdot(\frac{v}{n}+ p \cdot \frac{2\pi }{n}) }, \; p=0,1,2,...,n-1$

Her er n = 3, r = 8 og v = 0. Man får:

$z^n =8\Leftrightarrow z=\sqrt[3]{8}\cdot e^{i\cdot(p \cdot \frac{2\pi }{3}) }, \; p=0,1,2\Leftrightarrow$

$z=2\cdot e^{i\cdot0 } \vee z=2\cdot e^{i\cdot \frac{2\pi }{3}} \vee z=2\cdot e^{i \cdot \frac{4\pi }{3} }\Leftrightarrow$

$z=2 \vee z=2\cdot e^{i \cdot \frac{2\pi }{3}} \vee z=2\cdot e^{i \cdot \frac{4\pi }{3} }\Leftrightarrow$

$z=2 \vee z=2\cdot (cos(\tfrac{2\pi }{3})+i \cdot sin(\tfrac{2\pi }{3})) \vee z=2\cdot (cos(\tfrac{4\pi }{3})+i \cdot sin(\tfrac{4\pi }{3}))\Leftrightarrow$

$z=2 \vee z=2\cdot (-\tfrac{1}{2}+i \cdot \tfrac{\sqrt{3}}{2})) \vee z=2\cdot (-\tfrac{1}{2}-i \cdot \tfrac{\sqrt{3}}{2})) \Leftrightarrow$

$z=2 \vee z=-1+i \cdot \sqrt{3} \vee z=-1-i \cdot \sqrt{3}$

Hvis du prøver dig frem får du:

$(-1+i \cdot \sqrt{3})^3=(-1+i \cdot \sqrt{3}) \cdot(-1+i \cdot \sqrt{3}) \cdot (-1+i \cdot \sqrt{3})=$

$((-1)^2+2\cdot(-1)\cdot (i \cdot \sqrt{3}) +(i\cdot \sqrt{3})^2) \cdot (-1+i \cdot \sqrt{3})=$

$(-2-2\cdot i \cdot \sqrt{3}) \cdot (-1+i \cdot \sqrt{3})=$

$(-2)\cdot (-1)+(-2)\cdot (i \cdot \sqrt{3})+(-2\cdot i \cdot \sqrt{3})\cdot (-1)+(-2\cdot i \cdot \sqrt{3})\cdot (i \cdot \sqrt{3})=$

$2-2\cdot i \cdot \sqrt{3}+2\cdot i \cdot \sqrt{3}+2\cdot 3)=2+6=8$

Dvs første forslag er en løsning.

Brugbart svar (0)

Svar #8
24. september 2020 af Capion1

Med 6 svarmuligheder kunne opgaven være en del af en multiple choice test, hvor der ikke gives overflod af tid til at udpege det rigtige svar.
Med # 4 som elementær viden kan man straks se,
at (2) kan udelukkes, da (- 2)³ ikke kan være positiv
at (3), (4) og (6) kan udelukkes p.g.a. fortegnene
at (5) ikke har længden 2
Man må da have tillid til (1), såfremt opgaven ikke indeholder trykfejl.

Skriv et svar til: Hvilket komplekst tal er løsning til ligningen z^3=8

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.