Matematik

320. f’(x0)

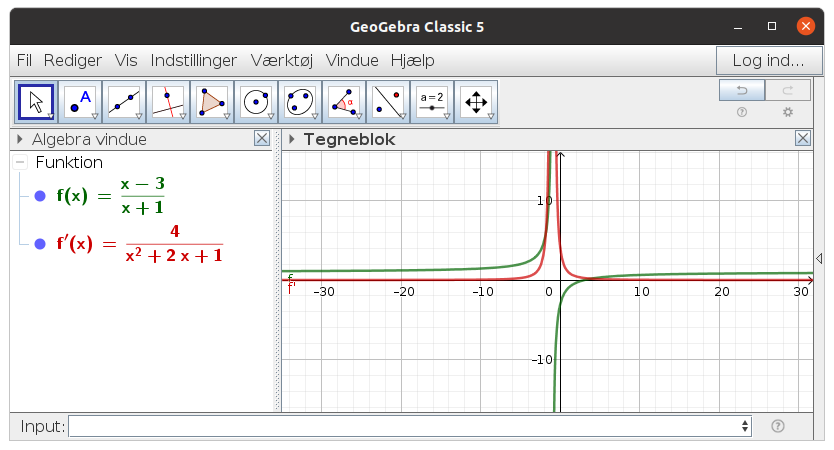
24. oktober 2020 af javannah5 - Niveau: A-niveau

Hvordan bestemmer jeg f’(x0) af dette tilfælde:
x-3/x+1

Brugbart svar (0)

Svar #1
24. oktober 2020 af peter lind

f(x) = x+1 - 3/x

f'(x) = 1 + 3/x²

Brugbart svar (0)

Svar #2
24. oktober 2020 af StoreNord

#0 Mon der menes:
(x-3)/(x+1 )

Brugbart svar (0)

Svar #3
24. oktober 2020 af Anders521

#0 Som nævnt i din anden tråd, brug din formelsamling, specifik. nr. (122), (123), (128), (133) og (134).

Svar #4
25. oktober 2020 af javannah5

Jeg har regnet det ud.
Er det rigtigt?

Vedhæftet fil:3F9D8306-8DA3-4B8D-BAAE-616CE9B81944.jpeg

Brugbart svar (0)

Svar #5
25. oktober 2020 af StoreNord

#0
Du har stadig ikke bekræftet at f(x) = (x-3)/(x+1).

Men hvis jeg havde ret, har du beregnet f'(x) rigtigt.

Brugbart svar (0)

Svar #6
25. oktober 2020 af StoreNord

Vedhæftet fil:Skærmbillede fra 2020-10-25 15-37-26.png

Brugbart svar (0)

Svar #7
25. oktober 2020 af ringstedLC

Der formodes:

$\begin{align*} f(x) &= \frac{x-3}{x+1}\;,\;x\neq -1 \\ &= (x-3)\cdot \frac{1}{x+1} \\ f(x) &= g(x)\cdot h\bigl(j(x)\bigr)\;\left\{\begin{matrix} g(x)&=&x-3&\Rightarrow &g'(x)&=&1\\ h(x)&=&\frac{1}{x}&\Rightarrow &h'(x)&=&-\frac{1}{x^2}\\ j(x)&=&x+1&\Rightarrow &j'(x)&=&1 \end{matrix}\right. \\ f'(x) &= g'(x)\cdot h\bigl(j(x)\bigr)+g(x)\cdot \Bigl(h\bigl(j(x)\bigr)\Bigr)' \\ &= g'(x)\cdot h\bigl(j(x)\bigr)+g(x)\cdot h'\bigl(j(x)\bigr)\cdot j'(x) \\ &= 1\cdot \frac{1}{x+1}+(x-3)\cdot \left(-\frac{1}{(x+1)^2}\right)\cdot 1 \\ &= \frac{1}{x+1}-\frac{x-3}{(x+1)^2} \\ f'(x) &= \frac{x+1-x+3}{(x+1)^2} = \frac{4}{(x+1)^2}\\ \end{align*}$

Brugbart svar (0)

Svar #8
25. oktober 2020 af ringstedLC

Anskaf dig en ternet eller hvid blok og find ud af, hvordan du holder kameraet, så billedet vender rigtigt.

$\begin{align*} \frac{f'(x_0)\,g(x_0)-f(x_0)\,g'(x_0)}{g(x_0)^2} &\;{\color{DarkGreen} =} \;\text{, er lig ?, det kan ikke v\ae re } f'(x)\\ \frac{{\color{Red} (x-3)}\,(x+1)-(x-3)\,{\color{Red} (x+1)}}{(x+1)^2} &= \text{, hvordan f\aa s de r\o de ?} \\ \frac{{\color{Red} 1\,\cdot }\,(x+1)-(x-3)\,{\color{Red} \cdot \,1}}{(x+1)^2} &= \text{, hvordan f\aa s de r\o de ?} \\ \text{For \o vrigt}: \frac{(x-3)\,(x+1)-(x-3)\,(x+1)}{(x+1)^2} &= \frac{(x-3)-(x-3)}{x+1}=0 \end{align*}$

Hvis du indskriver dette og aflevere det, vil du måske få nogle point for resultatet...

Skriv et svar til: 320. f’(x0)

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.