Matematik
stationær maple
jeg er igang med at løse denne opgave, men syns min besvarelse ser lidt forkert ud
Svar #1
28. oktober 2020 af nana2020
besvarelse ved ikke hvad de mener med rootof
Svar #2
28. oktober 2020 af nana2020
her kommer grafen
Svar #3
28. oktober 2020 af Soeffi
#0.

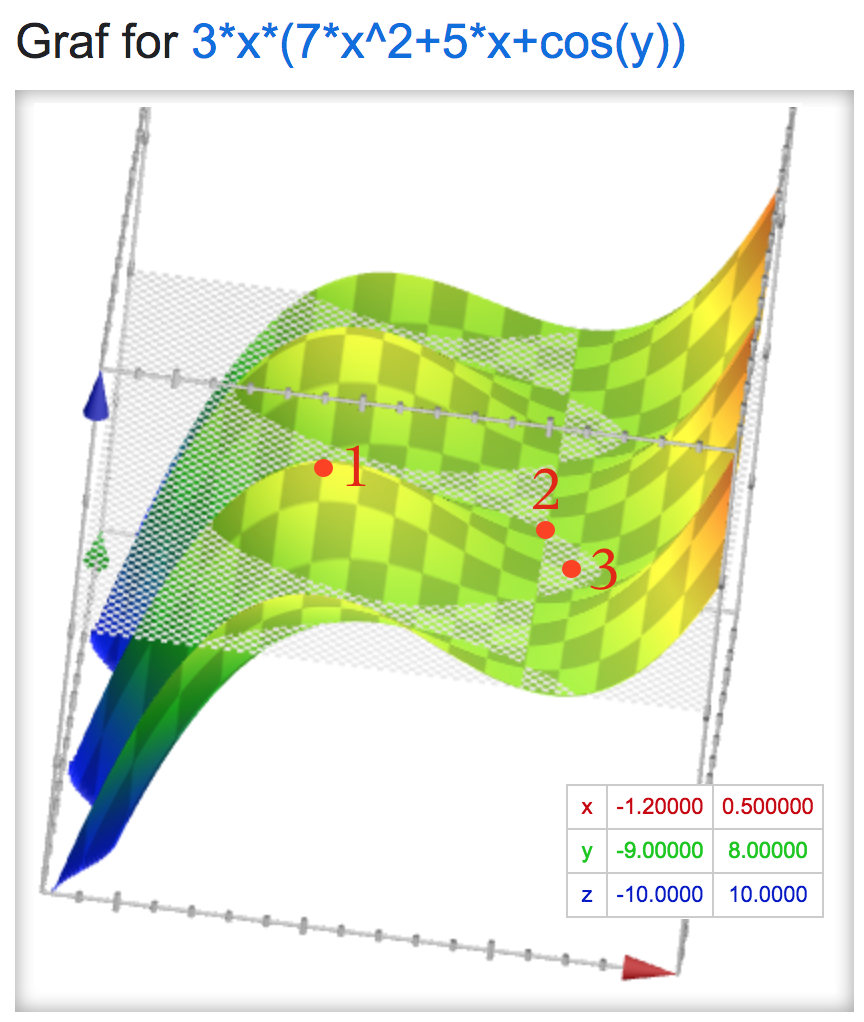
1: Maksimum, 2: Saddelpunkt, 3:Minimum. Disse gentager sig periodisk i y-aksens retning for hvert sin x-værdi.
Svar #5
28. oktober 2020 af Soeffi
#4. Der er faktisk et saddelpunkt mere. Det ligger på samme x-værdi, som det andet.
Stationære punkter:

Maksimumspunkter (at dømme efter figuren): (x,y) = (-1/3,2·p·π)
Minimumspunkter (at dømme efter figuren): (x,y) = (-1/7,2·p·π)
Saddelpunkter (at dømme efter figuren): (x,y) = (-0,561;(2·p+1)·π) og (x,y) = (0,0849;(2·p+1)·π)
p ∈ Z.
Svar #7
28. oktober 2020 af nana2020
jeg kan se vores resultater er i overstemmelse med hinanden med hvorfor for jeg rootOf hvordan kan de omskrives
Svar #8
28. oktober 2020 af Soeffi
#7.
Det er sandt, der er også de stationære punkter: (x,y) = (0,(2·p-1)·π/2), p ∈ Z. Dem overså jeg. Formodentlig saddelpunkter, men det kræver en nærmere undersøgelse.
Svar #9
29. oktober 2020 af Soeffi
#7...Prøv evt:
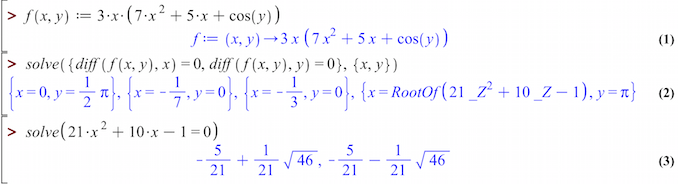
Svar #10
29. oktober 2020 af Soeffi
#3. Rettelse til Google-graf:
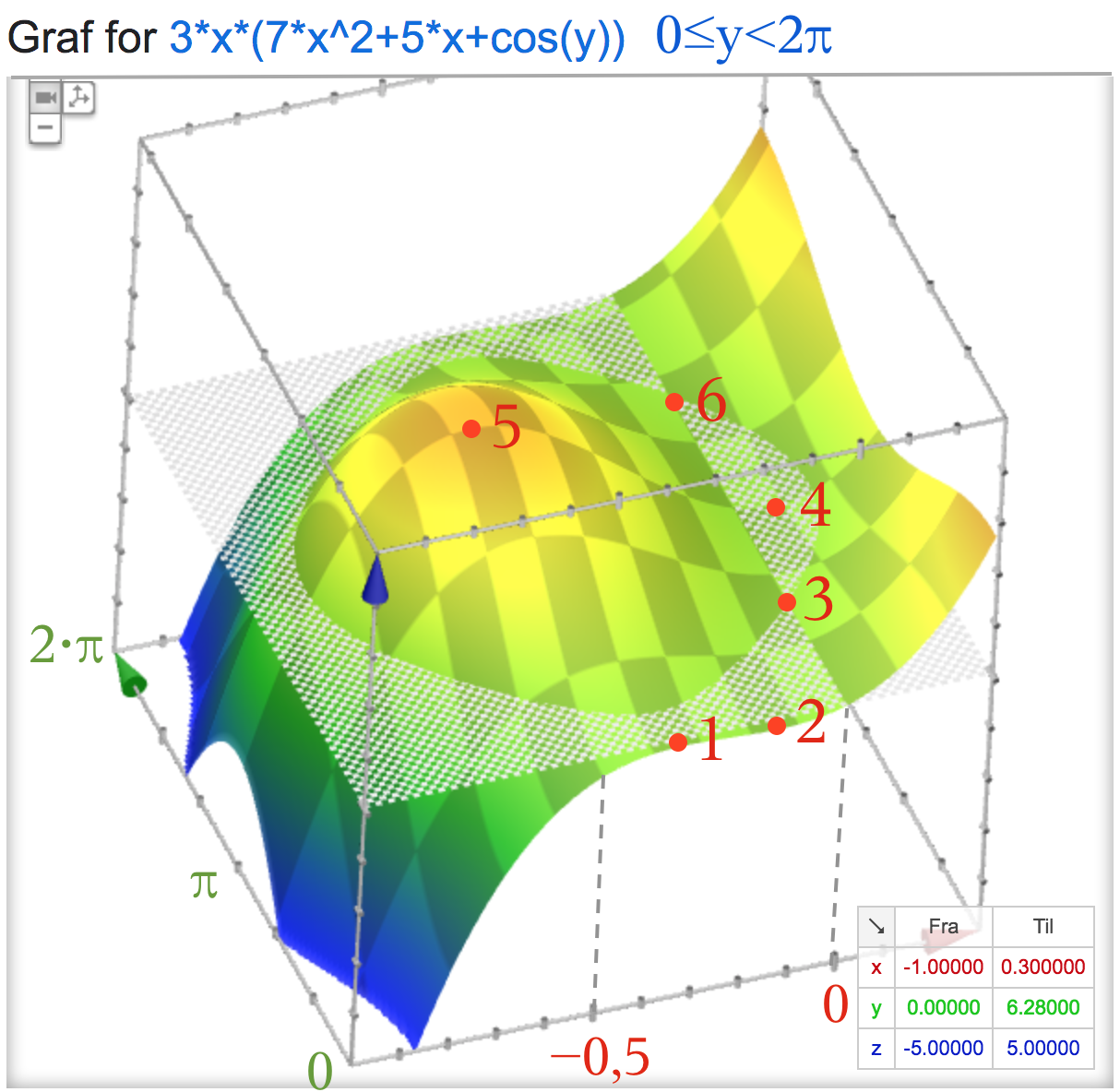
Stationære punkter for 0 ≤ y < 2π (gentages med perioden 2π):
1. (x,y) = (-1/3,0) (ligner saddelpunkt)
2. (x,y) = (-1/7,0) (ligner saddelpunkt)
3. (x,y) = (0,π/2) (ligner saddelpunkt)
4. (x,y) = (0,08;π) (ligner minimum)
5. (x,y) = (-0,56;π) (ligner maksimum)
6. (x,y) = (0,3π/2) (ligner saddelpunkt)
Skriv et svar til: stationær maple
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.

