Fysik

05. januar 2021 af Onana000 - Niveau: A-niveau

Hvordan løser jeg denne opgave?

Vedhæftet fil: 135797419_629355391121833_585007769621781527_n.jpg

Brugbart svar (0)

Svar #1
05. januar 2021 af Eksperimentalfysikeren

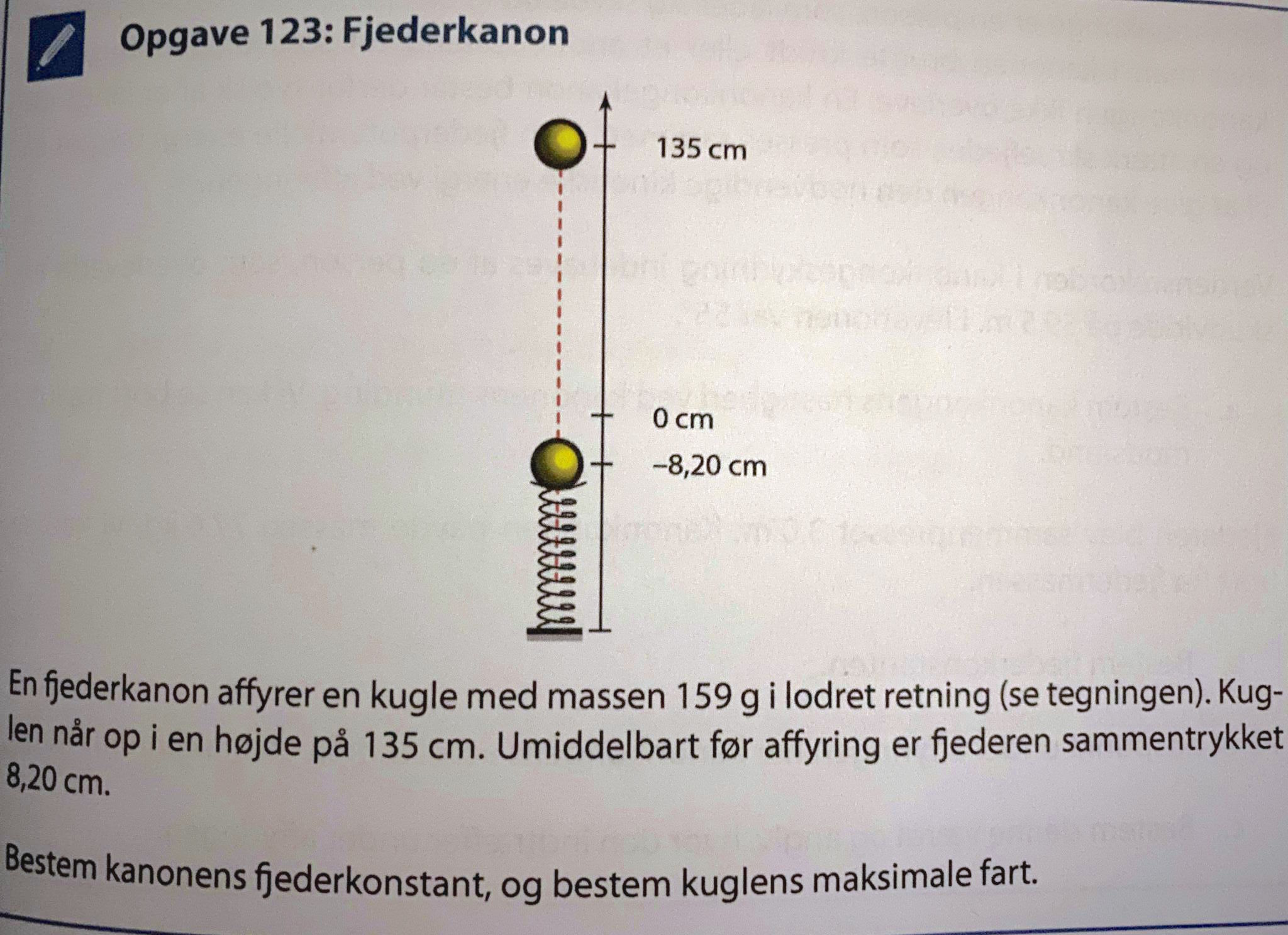
Find kuglens potentielle energi i højden 135cm. Bestem den også i -8,20cm. De to energer er lige store. I udftrykket for energien ved -8,20cm indgår fjederkonstanten. Den isolerer du.

Svar #2
05. januar 2021 af Onana000

Hvordan finder man så den maksimale fart for kuglen? Hvilken formel skal man bruge

Brugbart svar (0)

Svar #3
05. januar 2021 af Eksperimentalfysikeren

I højden 0 er al energien omsat til kinetisk energi.

Brugbart svar (0)

Svar #4
06. januar 2021 af mathon

$\small \begin{array}{lllll} \textup{Fjederenergi:}&E_{\textup{fjeder}}=\frac{1}{2}\cdot k\cdot x^2 \end{array}$

Der regnes uden energitab:

Fjederen afleverer ved afskydningen sin energi til kuglen som kinetisk energi.

Kuglens mekaniske energi er bevaret:
$\small \begin{array}{lllll} &E_{mek}=\frac{1}{2}\cdot m\cdot {v_1}^2+m\cdot g\cdot h_1=\frac{1}{2}\cdot m\cdot {v_2}^2+m\cdot g\cdot h_2\\\\& \frac{1}{2}\cdot k\cdot {\Delta x}^2+m\cdot g\cdot h_1=\frac{1}{2}\cdot m\cdot {v_2}^2+m\cdot g\cdot h_2 \end{array}$

Da højdens nulpunkt er lig med h₁
og v₂ er lig med nul,
har du:

$\small \begin{array}{lllll} \\\\& \frac{1}{2}\cdot k\cdot {\Delta x}^2=m\cdot g\cdot h_2\\\\& k=\frac{m\cdot g\cdot h_2}{\frac{1}{2}\cdot {\Delta x}^2}\\\\& \end{array}$

Brugbart svar (0)

Svar #5
06. januar 2021 af Soeffi

#0.

Vedhæftet fil:1992345.jpg

Skriv et svar til: Fysik

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.