Matematik

Vektorer

08. april 2021 af lauhan (Slettet) - Niveau: B-niveau

Hej. Jeg har lidt svært ved at forstå denne opgave, er der en der kan hjælpe mig?

Billedet er vedhæftet til spørgsmålet

Tak på forhånd

Vedhæftet fil: Skærmbillede 2021-04-08 kl. 21.38.01.png

Brugbart svar (0)

Svar #1
08. april 2021 af ringstedLC

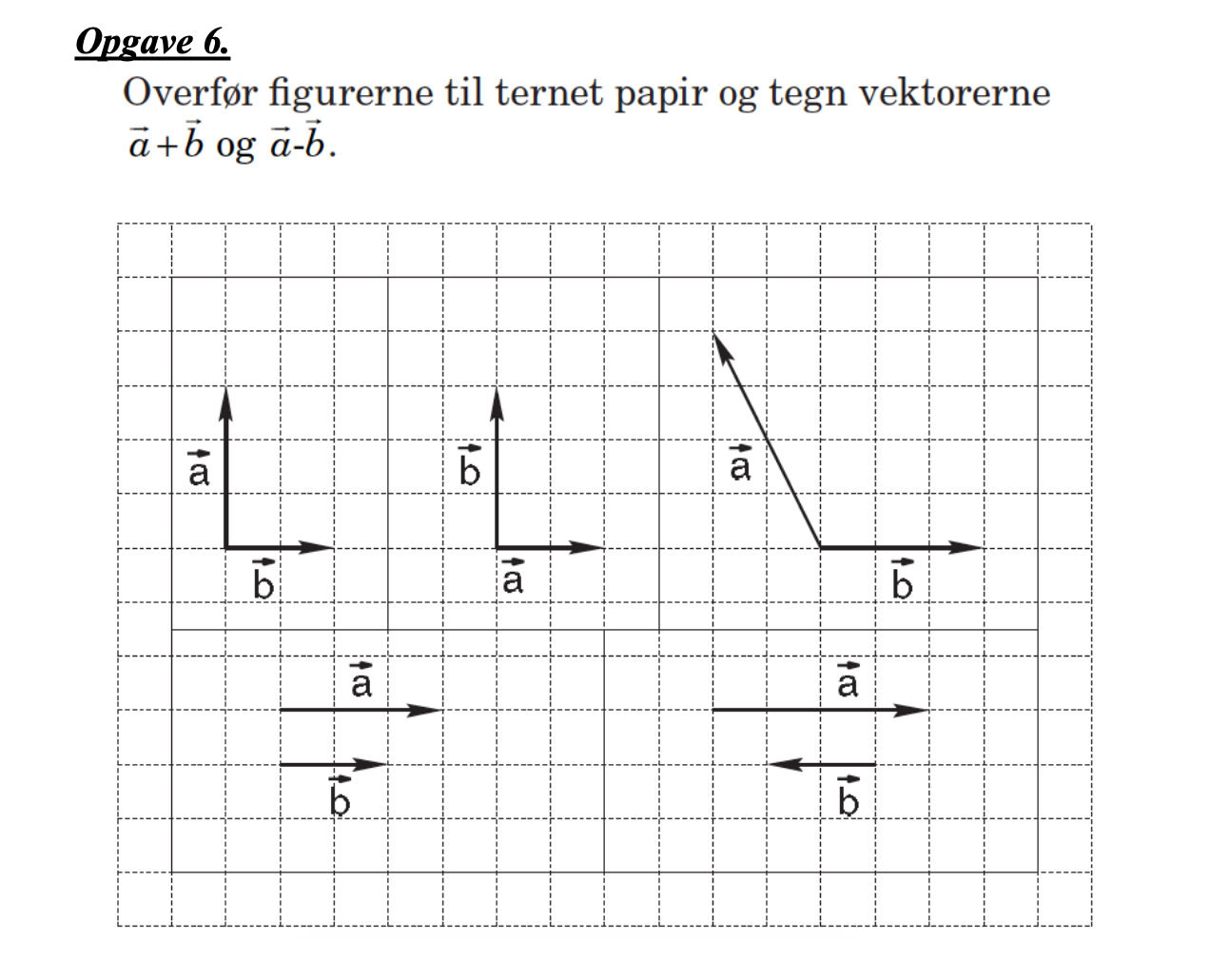
Aflæs vektor a og vektor b's koordinater:

$\begin{align*} \vec{a}+\vec{b} &= \binom{a_1+b_1}{a_2+b_2}=\binom{?}{?} \end{align*}$

og tegn resultatet. Eller med andre ord; hvor ender man, hvis man først går vektor a og derefter vektor b.

Brugbart svar (0)

Svar #2
08. april 2021 af AMelev

Se FS side 11 (47) & (48)

Svar #3
09. april 2021 af lauhan (Slettet)

Men jeg har svært ved at aflæse, hvilket et af vektorene der er a og b

Svar #4
09. april 2021 af lauhan (Slettet)

Altså er der ikke nogen der please kan forklare og regne det ud, har brug for hjælp

Brugbart svar (0)

Svar #5
09. april 2021 af mathon

Vektorer adderes/subtraheres geometrisk.

Vektorsum og vektordifferens er diagonalerne i det parallellogram vektorerne udspænder.
.

Kendes koordinaterne anvendes
$\small \begin{align*} \vec{a}\pm\vec{b} &= \binom{a_1\pm b_1}{a_2\pm b_2} \end{align*}$

Brugbart svar (1)

Svar #6
09. april 2021 af PeterValberg

Måske dette kan "pege" dig i den rigtige retning

- - -

mvh.

Peter Valberg
(YouTube)

Vedhæftet fil:Unavngivet.png

Brugbart svar (1)

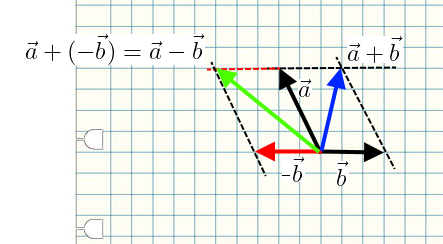
Svar #7
09. april 2021 af AMelev

#4 Der står jo angivet ved vektorerne, hvad de enkelte vektorer hedder.
En vektor er kendetegnet ved længde og retning, så alle pile med samme længde og retning repræsenterer en og samme vektor.

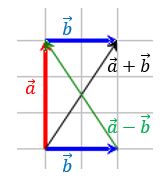
Sumvektor $\vec a +\vec b$ :
Læg en repræsentant for $\vec b$ i spidsen af $\vec a$ og tegn vektoren fra starten af $\vec a$ til spidsen af $\vec b$ .

Differensvektor $\vec a -\vec b$ :
Læg repræsentanter for de to vektorer med samme startpunkt og tegn vektoren fra spidsen af $\vec b$ til starten af $\vec a$ .

Eksempel jf. Formelsamling side 11 (47) & (48)

Vedhæftet fil:Udklip-1.JPG

Svar #8
09. april 2021 af lauhan (Slettet)

men kan i skrive det med tallene

Svar #9
09. april 2021 af lauhan (Slettet)

tusind tak

Svar #10
09. april 2021 af lauhan (Slettet)

Men er a+b så (2,3) og a-b (-2,3)??

Brugbart svar (1)

Svar #11
09. april 2021 af AMelev

#10 Ja i eksemplet i #7.
Egentlig skriver man koordinaterne for vektorer over hinanden for at kunne skelne dem fra punkter, men det er af mindre betydning.
$\vec a=\binom{0}{3},\, \vec b=\binom{2}{0},\, \vec a+\vec b=\binom{2}{3} \, \textup{og}\: \vec a-\vec b=\binom{-2}{3}$

Svar #12
09. april 2021 af lauhan (Slettet)

taaaak

Skriv et svar til: Vektorer

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.