Matematik
find radius af en cylinder i en kegle
Hey:)
Jeg har fået en opgave, som jeg ikke kan finde ud af, opgaveformularingen lyder sådan:
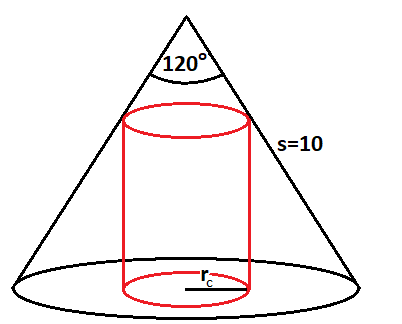
find rc af cylderen, der giver cylinderen den størst mulige volume, Vc, så den passer ind i keglen med denne volume. Vi får at vide: keglen: sideløngde= s=10, vinklen v=120, og så en cylinder med radius rc
vedheft er billede af cylinderen og keglen.
Jeg håber at i kan hjælpe mig, takk:)
Svar #2
01. maj 2021 af peter lind
Sidefladerne sammen med radius danner en ligesidet trekant. Brug pytagoras til finde radius af bunden af keglen r. Vc = π*rc2*h, hvor h er højden, Højden kan findes af trekanten der dannes af højden og siden på bunden der er r-rc
Svar #4
02. maj 2021 af ringstedLC
#0: Det er lidt uklart, hvad opgaven går ud på. Vedhæft gerne et godt billede af hele opgaven.
det kan jeg godt, men det er på færøersk. Men det som jeg skal finde er radius af cylinderen rc, altså hvor lang radius er
her er hele opgave, måske fortsår i noget.
Bare sig til hvis jeg skal oversætte noget
#2
skal jeg så sige c2=102+102 eller er det ommvendt phytagoros? altså c2=102-102?
Svar #8
02. maj 2021 af ringstedLC
#2: "Sidefladerne sammen med radius danner en ligebenet trekant".
#7: Der findes ikke nogen "omvendt" Pythagoras. Med #3 kan du beregne rk og hk
#6: Så lærte jeg også at tolke lidt færøsk.
Oversættelse af den sidste sætning: ", og således at cylinderen kan være indeni keglen vio hesari volumu", har du oversat til: med denne volume.
Det er en optimeringsopgave:
Svar #9
02. maj 2021 af Soeffi
#6.
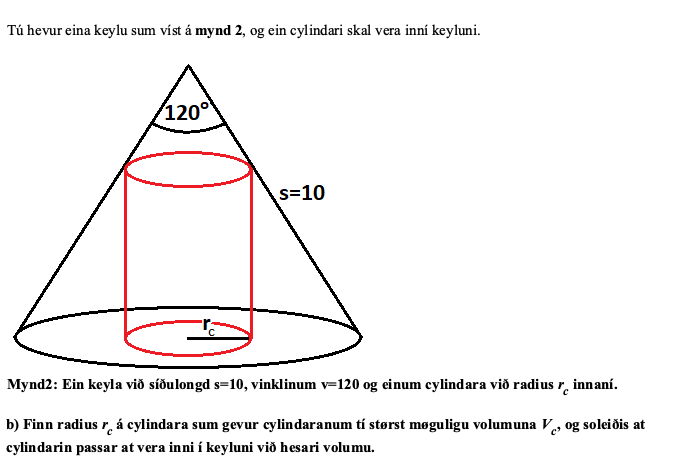
Du har en kegle som vist på figur 2, og en cylinder indskrevet i denne.
Figur 2: En kegle med sidelængde s=10, (top)vinkel v=120° og en cylinder med radius rc.
b) Find den radius rc, der giver cylinderen det størst mulige volumen Vc.
Svar #13
05. maj 2021 af ringstedLC
Du må være mere konkret i dine spørgsmål, der står jo flere ting i #8. Fx "Jeg forstår ikke hvorfor tan(30º) = ...
ja jeg forstår gott at tan(30)=hc/rk-rc, men hvorfor bliver det pludseligt rk=10·cos(30)?, jeg ved at rk så er 1,5, men hvordan?
og så forstår jeg heller ikke, hvordan hc pludselig giver tan(30)•(10•cos(39)-rc)
Og også hvad de mener med V(rc)
Svar #15
06. maj 2021 af Soeffi
#14...ja jeg forstår gott at tan(30) = hc/(rk-rc), men hvorfor bliver det pludseligt rk = 10·cos(30)?
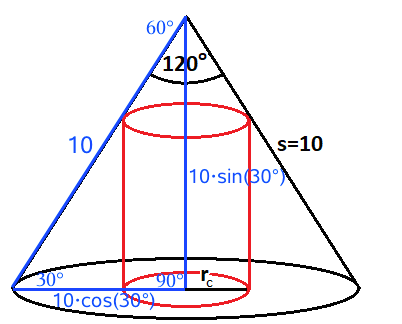
Det fremgår af tegningen, at keglens radius er 10·cos(30°) = 8,66.
...og så forstår jeg heller ikke, hvordan hc pludselig giver tan(30°)•(10•cos(30°)-rc)...
Du forstod: tan(30°) = hc/(rk-rc)...dette medfører: hc = tan(30°)·(rk-rc) ⇒ hc = tan(30°)·(10•cos(30°)-rc)
Og også hvad de mener med V(rc)
V(rc) = Vc
jeg prøvede at regne hc ud, men det virker rigtig forkert
er det her rætt:
V(rc)=π · r2c· hc
og så skal jeg bare differentiere det?, og putte det ligmed 0, og so er det svaret?
og så gjorde jeg det her, for at regne volumen
det er sikkert meget forkert, jeg synes bare at det er rigtig svært at forstå
Svar #19
07. maj 2021 af peter lind
Du kan se direkte hvad hc er på tegningen i #14 og og formlen for udregningen af rc står også i #14