Side 2 - find radius af en cylinder i en kegle - Matematik

Brugbart svar (0)

Svar #21
07. maj 2021 af peter lind

nej da. Der står at h_c = 10sin(30º)

Svar #22
07. maj 2021 af 927

hvordan finder jeg så rc?

Brugbart svar (0)

Svar #23
07. maj 2021 af peter lind

sæt h_c ind i den sidste ligning i #14 og isoler r_c

Svar #24
07. maj 2021 af 927

#21 er du sikker at hc er 10·sin(30)? er det ikke hk, altså højden på keglen?

Brugbart svar (0)

Svar #25
07. maj 2021 af peter lind

Ja. se selv på figures venster side. hk = 10sin(60º)

Svar #26
07. maj 2021 af 927

undskyld men nu er lidt forvirret

du siger at jeg skal sætte hc ind, og det forstår jeg godt, men jeg ved ikke hvad hc er endn, jeg ved kun hvad hk er, hvordan finder jeg så hc

Brugbart svar (0)

Svar #27
07. maj 2021 af peter lind

se #21

Jeg synes at du skulle reptere hvad vi er kommet frem til. Du spørger jo om noget vi ha svaret på tidligere

Brugbart svar (0)

Svar #28
07. maj 2021 af ringstedLC

Bemærk: Opgavens figur er stærkt misvisende, da keglens topvinkel er vist spids, men angivet til 120º:

$\begin{align*} h_k &= 10\cdot \sin(30^{\circ}) \\ r_k &= 10\cdot \cos(30^{\circ}) \end{align*}$

Vedhæftet fil:__0A.png

Svar #29
07. maj 2021 af 927

men hvordan kan hc og hk være det samme= 10·sin(30)?

Svar #30
07. maj 2021 af 927

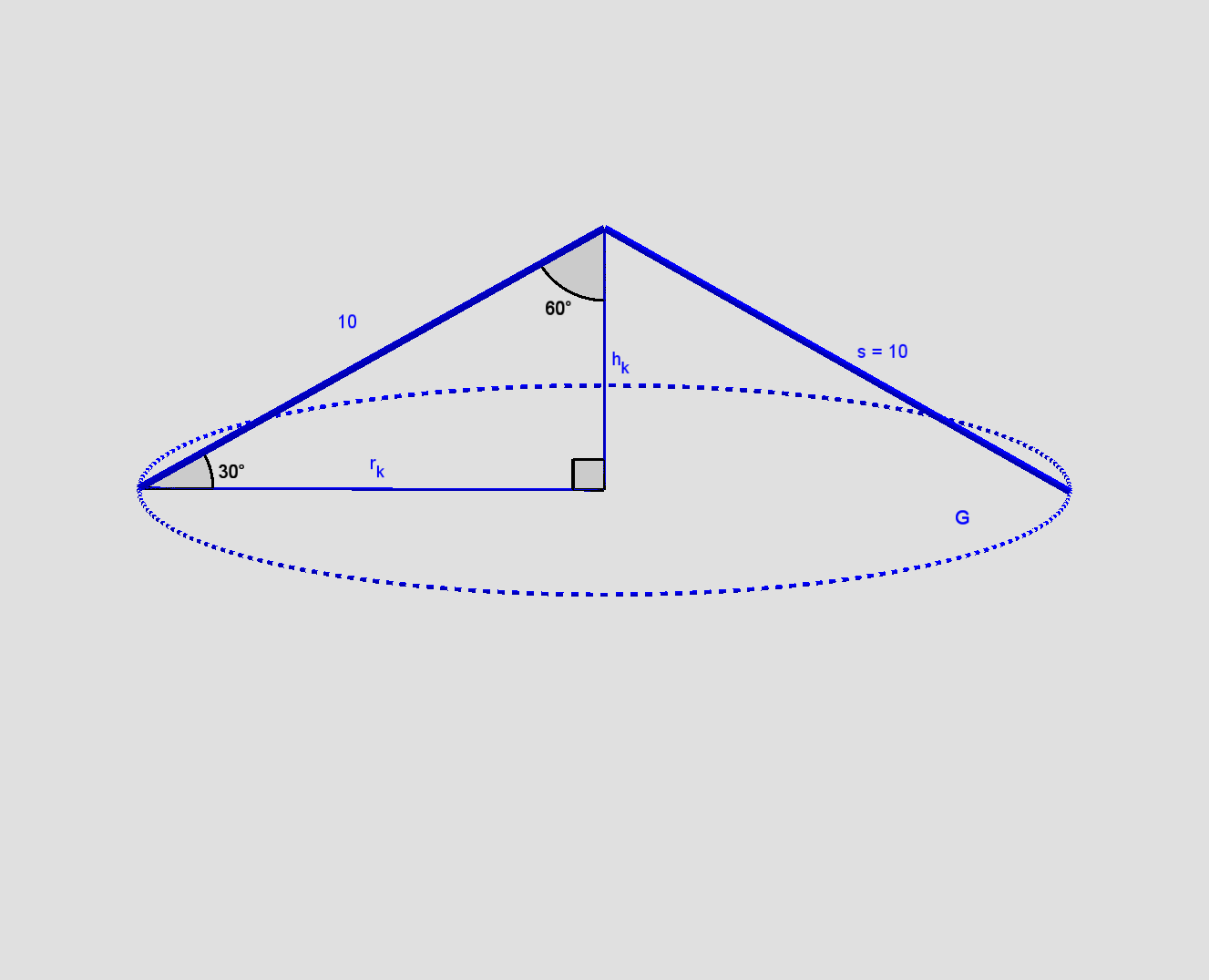
hk er højden af keglen ikke? og hc er højden af cylinderne, men de kan da ikke være det samme eller?

Brugbart svar (1)

Svar #31
07. maj 2021 af peter lind

h_k = 10sin(60º)

h_c = 10sin(30º)

Det er ikke det samme!!

Tag lige og slap af. Du skal samle det du har fået at vide sammen og skrive det ned. Også hvad du skal gøre

Svar #32
07. maj 2021 af 927

Takk:)

Svar #33
07. maj 2021 af 927

men i #28 skrev du at hk var 10·sin(30) det var derfor jeg blev lidt forvirret

Brugbart svar (0)

Svar #34
07. maj 2021 af Soeffi

#23.

V_c = (10·tan(30°)·cos(30°) - tan(30°)·r_c)·π·r_c².

V'_c = (20·tan(30°)·cos(30°) - 3·tan(30°)·r_c)·r_c·π.

V'_c = 0 ⇒ r_c = 0 ∨ r_c = (20·tan(30°)·cos(30°))/(3·tan(30°)) = (20/3)·cos(30°) = 5,77.

Brugbart svar (1)

Svar #35
07. maj 2021 af ringstedLC

#33: Du forveksler os, der hjælper. Og jeg kan heller ikke forstå #21 m.m.

Uddybning af #8:

$\begin{align*} h_c &= \tan(30^{\circ})\cdot \left (r_k-r_c \right ) \\ &= \tan(30^{\circ})\cdot \left (10\cdot \cos(30^{\circ})-r_c \right ) \\ V &= \pi\cdot {r_c}^2\cdot h_c \\ V(r_c)&= \pi\cdot {r_c}^2\cdot \tan(30^{\circ})\cdot \left (10\cdot \cos(30^{\circ})-r_c \right ) \\ \end{align*}$

Så har du cylinderens volume som en funktion alene af radius. Differentier den og løs:

$\begin{align*} V'(r_c)=0&= ... \Rightarrow r_c=\;? \end{align*}$

Vedhæftet fil:__0B.png

Brugbart svar (0)

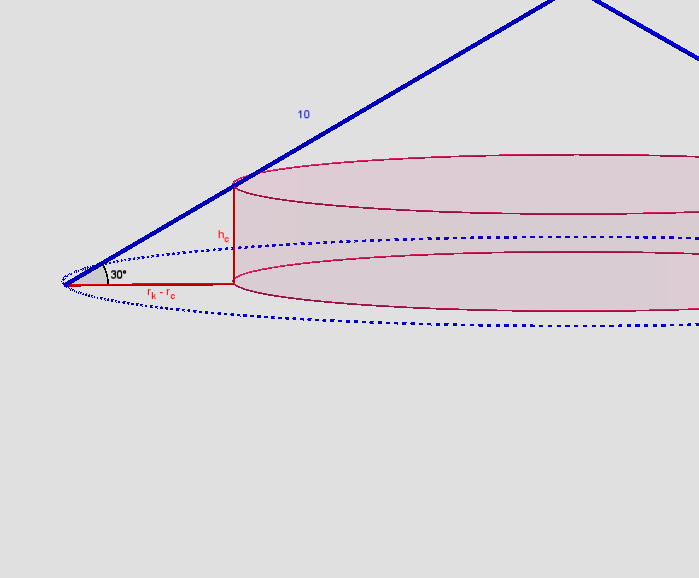
Svar #36
08. maj 2021 af Soeffi

#34. Kan skrives:

V_c = tan(30°)·π·(r_k·r_c² - r_c³).

V'_c = tan(30°)·π·r_c·(2·r_k - 3·r_c)

V'_c = 0 ⇒ r_c = 0 ∨ r_c = (2/3)·r_k.

Dvs. for en hvilken som helst (lige) kegle vil den størst mulige indskrevne cylinder have en radius, der er 2/3 af keglens.

Svar #37
08. maj 2021 af 927

tusind takk!!! betyder det så, at der ikke er et rigtig tal, som er svaret?

Svar #38
08. maj 2021 af 927

nu er jeg lidt forvirret igen:

#34 siger at Vc = (10·tan(30°)·cos(30°) - tan(30°)·rc)·π·rc2.

#35 siger at V(r_c)=Π·r^2·tan(30)·(10·cos(30)-r_c)

og #36 siger noget helt andet, at Vc = tan(30°)·π·(rk·rc2 - rc3).

alt er ikke rigtig det samme, hvad er best at skrive? Selv synes jeg at #34 giver mere mening, fordi at hc=tan(30)·(10·cos(30)-rc)

Brugbart svar (0)

Svar #39
08. maj 2021 af ringstedLC

#38: Omskriv lidt på forskrifterne:

$\begin{align*} \textup{\#34}:V_c &= \Bigl(10\cdot \tan(30^{\circ})\cdot \cos(30^{\circ})-\tan(30^{\circ})\cdot r_c\Bigr)\cdot \pi\cdot {r_c}^2 \\ &= \Bigl(10\cdot \cos(30^{\circ})-r_c\Bigr)\cdot \tan(30^{\circ})\cdot \pi\cdot {r_c}^2 \\ \textup{\#35}:V(r_c) &= \pi \cdot {r_c}^2\cdot \tan(30^{\circ})\cdot \Bigl(10\cdot \cos(30^{\circ})-r_c\Bigr) \\ \textup{\#34}:V_c &= \Bigl(\underset{r_k}{\underbrace{10\cdot \cos(30^{\circ})}}-r_c\Bigr)\cdot \tan(30^{\circ})\cdot \pi\cdot {r_c}^2 \\ &= \Bigl(r_k\cdot {r_c}^2-r_c\cdot {r_c}^2\Bigr)\cdot \tan(30^{\circ})\cdot \pi \\ &= \Bigl(r_k\cdot {r_c}^2-{r_c}^3\Bigr)\cdot \tan(30^{\circ})\cdot \pi \\ \textup{\#36}:V_c &= \tan(30^{\circ}) \cdot \pi \cdot \Bigl(r_k\cdot {r_c}^2-{r_c}^3\Bigr) \\ \end{align*}$

#34, #35 og #36 giver altså det samme.

Svar #40
08. maj 2021 af 927

så det er ligemeget hvilken jeg vælger? så vælger jeg den der giver mest mening for mig, tusind takk!1:D