Fysik

Bølger

08. maj 2021 af rycdi - Niveau: C-niveau

Hej er der nogen der kan hjælpe mig?

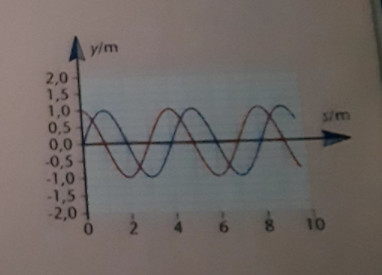
a) Tegn den resulterende bølge.

Hvordan skal den resulterende bølge se ud når de ligesom "går ud" med hinanden?

Vedhæftet fil: Screenshot_3.png

Brugbart svar (0)

Svar #1
08. maj 2021 af peter lind

Brugbart svar (0)

Svar #2
08. maj 2021 af peter lind

Du skal bare lægge ampplituderne sammen. Det ser ud til at den enener en sinusfunktion og den anden er en cosinus funktion med samme frekvens og amplitude. Hvis det er rigig er den resulterende bølge y = sin(ωt) + cos(ω) . Du kan bruge additionsformlerne for de trigonometriske funkioner for at gøre de mere læselig og forståelse

Brugbart svar (0)

Svar #3
08. maj 2021 af Eksperimentalfysikeren

Det er ikke amplituderne, der skal lægges sammen, men øjebliksværdierne.

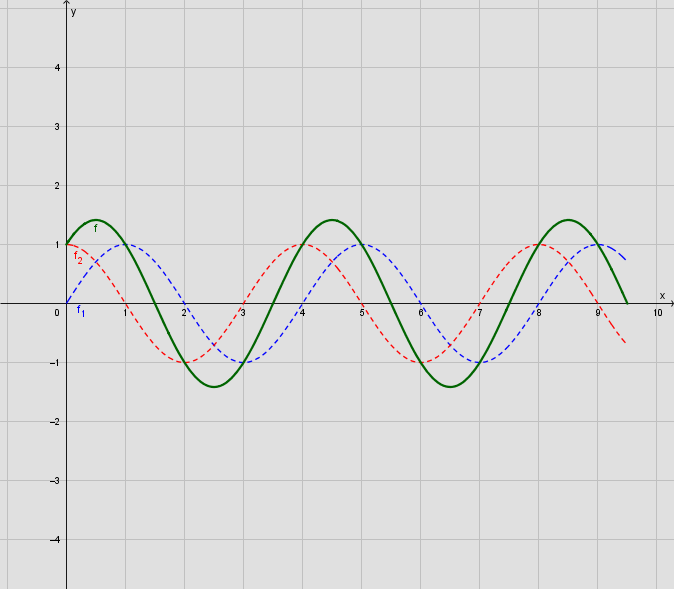
Vælg en række x-værdier. For hver af dem aflæser du de to kurvers y-værdi. De to værdier lægger du sammen og afsætter den samlede værdi som y-værdi for den resulterende bølge. Tegn kurven gennem punkterne.

Brugbart svar (0)

Svar #4
08. maj 2021 af ringstedLC

Vedhæftet fil:__3.png

Svar #5
09. maj 2021 af rycdi

Hej alle, jeg har prøvet mig frem.

De to bølger krydser hinanden ved 0,75 ad y-aksen, derefter ganger jeg 0,75 med 2 da det er en konstruktiv bølge, dermed bliver det 1,5 op ad y-aksen.

I forhold til bølgelængden er jeg lidt i tvilv om.

Brugbart svar (0)

Svar #6
09. maj 2021 af peter lind

Det kan du se af grafen i #4. Den er uændret. Hvis du antager sinusbølgen kan du som angivet i #1 også regne dig frem til det.

Brugbart svar (0)

Svar #7
09. maj 2021 af ringstedLC

#5: Der er ikke så ret mange "pæne" numeriske værdier til de trigonometriske funktioner. Brug eksakte værdier:

$\begin{align*} s_0=0 &\Rightarrow \left\{\begin{matrix}{\color{Blue} y_1=\sin(0^{\circ})=0} \\ {\color{Red} y_2=\cos(0^{\circ})=1}\end{matrix}\right. \quad y_1+y_2=y_0=1 \\ s_1=0.5 &\Rightarrow \left\{\begin{matrix}{\color{Blue} y_1=\sin(45^{\circ})=\frac{\sqrt{2}}{2}} \\ {\color{Red} y_2=\cos(45^{\circ})=\frac{\sqrt{2}}{2}}\end{matrix}\right. \quad y_1+y_2=y_{0.5}=\sqrt{2}\approx 1.41 \\ &...........................................\\ s_2=2.5 &\Rightarrow \left\{\begin{matrix}{\color{Blue} y_1=\sin(315^{\circ})=-\frac{\sqrt{2}}{2}} \\ {\color{Red} y_2=\cos(315^{\circ})=-\frac{\sqrt{2}}{2}}\end{matrix}\right. \quad y_1+y_2=y_{2.5}=-\sqrt{2}\approx -1.41 \\ s_3=4 &\Rightarrow \left\{\begin{matrix}{\color{Blue} y_1=\sin(360^{\circ})=0} \\ {\color{Red} y_2=\cos(360^{\circ})=1}\end{matrix}\right. \quad y_1+y_2=y_{4}=1=y_0\Rightarrow \textup{b\o lgel\ae ngden}=4 \\ \end{align*}$

På figuren i #4:

$\begin{align*} f_1(s) &=\sin\left (\tfrac{2\,\pi}{4}\,s \right )\;,\;0\leq s\leq 9.5 \\ f_2(s) &=\cos\left (\tfrac{2\,\pi}{4}\,s \right )\;,\;0\leq s\leq 9.5 \\ f(s)=f_1(s)+f_2(s) &=\sin\left (\tfrac{\pi}{2}\,s \right )+\cos\left (\tfrac{\pi}{2}\,s \right )\;,\;0\leq s\leq 9.5 \end{align*}$

Svar #8
09. maj 2021 af rycdi

Mange tak for jeres grundig svar.

Skriv et svar til: Bølger

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.