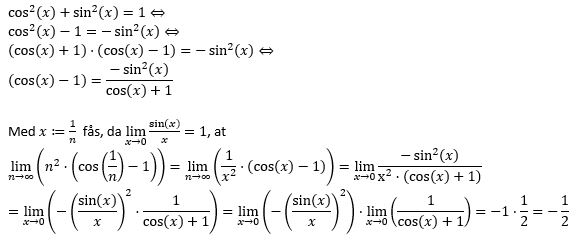Matematik

Konvergens og grænseværdi

10. maj 2021 af K22 - Niveau: Universitet/Videregående

Hej. Hvordan løser jeg denne opgave? Jeg har forsøgt at gøre det, og jeg ender med at få 0, men ifølge mit CAS-værktøj bør grænseværdien være -1/2.

Vedhæftet fil: Skærmbillede 2021-05-10 kl. 09.16.50.png

Brugbart svar (2)

Svar #1
10. maj 2021 af janhaa

$\lim \\ n\to \infty \,\,\,\,n^2*(\cos(1/n) - 1) =-1/2$

use Laurent series

Svar #2
11. maj 2021 af K22

slet

Brugbart svar (1)

Svar #3
11. maj 2021 af AMelev

#0
Produktreglen for grænseværdi gælder ikke, når den ene faktor går mod 0, og den anden går mod ∞ eller -∞.

Svar #4
11. maj 2021 af K22

Finder der en anden metode? Jeg har ikke haft om det før. Måske har det også et andet navn?

Brugbart svar (1)

Svar #5
11. maj 2021 af AMelev

Lidt pusleri førte frem til dette.

Vedhæftet fil:Udklip.JPG

Svar #6
11. maj 2021 af K22

Jeg synes, at det hele giver god mening, men hvordan får du den ide, at x := 1/n? Og hvorfor ændrer du n-> uendelig til x -> 0 ?

Brugbart svar (1)

Svar #7
11. maj 2021 af AMelev

Ideen kommer fra cos(1/n). At jeg har brugt x i stedet for 1/n er ren dovenskab - det er hurtigere at skrive og nemmere at overskue.

n→∞ ⇒ 1/n→0 ⇔ x→0.
Det burde have været ændret allerede i 2. trin, hvor x indsættes i stedet for 1/n.
En "kopi-pasta-smutter" :)

Svar #8
11. maj 2021 af K22

Mange tak for hjælpen :)

Brugbart svar (0)

Svar #9
11. maj 2021 af Soeffi

#1...

En pontens rækkeudvikling giver:

$\lim_{n\to \infty} \;n^2\cdot ({\color{Red} \cos(1/n)} - 1) =\lim_{n\to \infty} \;n^2\cdot ({\color{Red} 1-\frac{(1/n)^2}{2!}+\frac{(1/n)^4}{4!}-...} - 1) =$

$\lim_{n\to \infty} \;n^2\cdot (-\frac{(1/n)^2}{2!}+\frac{(1/n)^4}{4!}-...) =\lim_{n\to \infty} (-\frac{1}{2!}+\frac{(1/n)^2}{4!}-...) =-\frac{1}{2}$

Brugbart svar (0)

Svar #10
16. maj 2021 af AskTheAfghan

Alternativt, udtrykket kan omskrives til

n²(cos(1/n) - 1) = [cos(1/n) - 1]/(1/n²),

og til højre af denne ligning går både tælleren og nævneren mod 0, så kan man fordel benytte L'Hospitals regel; her er

[cos(1/n) - 1]'/(1/n²)' = (-1/2) sin(1/n)/(1/n) → -1/2, når n → ∞,

idet faktoren sin(1/n)/(1/n) går som bekendt mod 1 for n gående mod ∞.

Skriv et svar til: Konvergens og grænseværdi

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.