Matematik

Konvergens og grænseværdi

10. maj 2021 af K22 - Niveau: Universitet/Videregående

Hej. Jeg har brug for hjælp til denne opgave. Jeg får grænseværdien til ln(2) vha. CAS, men hvordan skal man vise det? Den eneste måde, at jeg kan få det til at gå op er, hvis grænserne er hhv. 1 og 2, når man skal udregne integralet af 1/x.

Vedhæftet fil: Skærmbillede 2021-05-10 kl. 09.19.25.png

Brugbart svar (1)

Svar #1
10. maj 2021 af janhaa

$Sum=\int_{0}^{1}\frac{1}{n+1}\,dn=\ln(1+n)|_0^1=\ln(2)$

Brugbart svar (1)

Svar #2
10. maj 2021 af AMelev

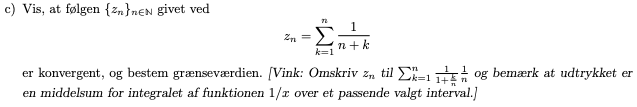
Jeg ville kalde det en højresum, men grænseværdien er den samme, så pyt.

Hvis du tager et interval [a,b] og opdeler i n lige store dele, er hver af dem $\Delta x=\frac{b-a}{n}$ og intervaldelepunkterne er dermed $x_k=a+k\cdot \Delta x$
Højresummen for $f(x)=\frac{1}{x}$ er så
$S_n=\sum_{k=1}^{n}f(a+k\cdot \Delta x)\cdot \Delta x = \sum_{k=1}^{n}\frac{1}{a+k\cdot \Delta x}\cdot \Delta x$ og $\lim_{n \to \infty }S_n=\int_{a}^{b}\frac{1}{x}dx$

Med a = 1 og b = 2, har du du det ønskede, $S_n=\ \sum_{k=1}^{n}\frac{1}{1+k\cdot \frac{1}{n}}\cdot \frac{1}{n}$ og dermed, at
$\lim_{n \to \infty }S_n= \lim_{n \to \infty }\sum_{k=1}^{n}\frac{1}{1+k\cdot \frac{1}{n}}\cdot \frac{1}{n}= \int_{1}^{2}\frac{1}{x}dx$

Svar #3
11. maj 2021 af K22

1# Må man gerne bruge x i stedet for n?

Brugbart svar (1)

Svar #4
11. maj 2021 af AMelev

Du må kalde variablen, hvad du har lyst til, men der er nok tradition for, at n mest benyttes til naturlige tal.

Svar #5
11. maj 2021 af K22

1# hvordan får du de grænser, og hvordan får du 1/n+1 ?

Brugbart svar (0)

Svar #6
16. maj 2021 af AskTheAfghan

Nu er den sidste del af opgaven besvaret (bemærk, at din sum er en Riemann sum i forklædning, derfor kan summen omskrives til et bestemt integral), så vil jeg hjælpe med den første del, hvis du skulle være interesseret. Lad n være et fast naturligt tal, og hvis k er et heltal opfyldende 1 ≤ k ≤ n, har man 1/(2n) ≤ 1/(n+k) ≤ 1/(1+n), og dermed er (1/2) ≤ z_n ≤ n/(n+1). Der ses nu let, at den voksende følge {z_n}_n er opadtil begrænset (af 1), så den konvergerer.

Skriv et svar til: Konvergens og grænseværdi

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.