Matematik
Vinkler i figuren, Ny Zigma, Opgave 9 098, Side 247 (Henry Schultz med flere)
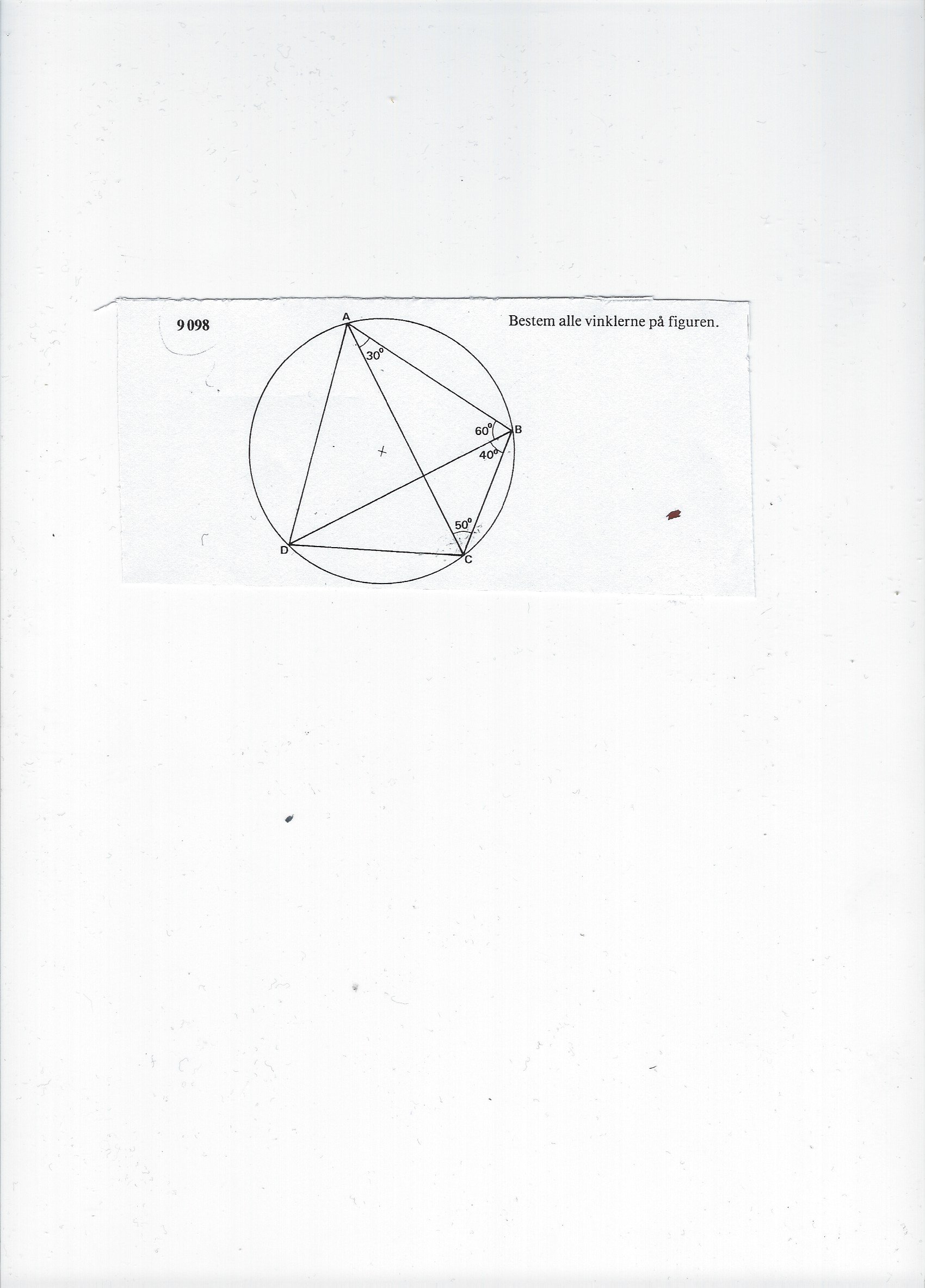
I den vedhæftede fil er der et billed af en cirklet hvor der er indtegnet en figur og i figuren er der oplyst nogle vinkler,
Opgaven består i at bestemme alle vinklerne på fuguren.
Mit spørgsmål er, hvordan bestemmer man alle vinklerne på figuren ?
På forhånd tak
Svar #2
19. september 2021 af mathon
Bemærk:
Skæringen mellem AC og BD danner fire rette vinkler.
Periferivinkler, der spænder over den samme bue, er lige store.
Svar #3
19. september 2021 af ca10
Tak for svaret
Jeg kan se at skæringen mellem AC og BD danner fire rette vinkler
Vinkel summen i en trekant altid er 1800 , og i en trekant, hvor de to vinkler er og den ukendte vinkel kalder jeg x
600 + 300 + x = 1800 , og x = 1800 - (600 + 300) = 900
I den anden trekant er de to vinkler og den ukendte vinkel er y
400 + 500 + y = 1800 og y = 1800 - (400 + 500) = 900
Så skæringen mellem AC og BD danner fire rette vinkler.
Så langt så godt.
Det næste svar forstår jeg ikke, periferivinkler, der spænder over den samme bue, er lige store, hvordan det skal bruges til løse opgaven, kan jeg ikke lige se.
Kan du evt give et tip til, hvordan det kan bruges til at løse opgave. Du må gerne give et eksempel på udregningen.
På for hånd tak
Svar #4
19. september 2021 af Eksperimentalfysikeren
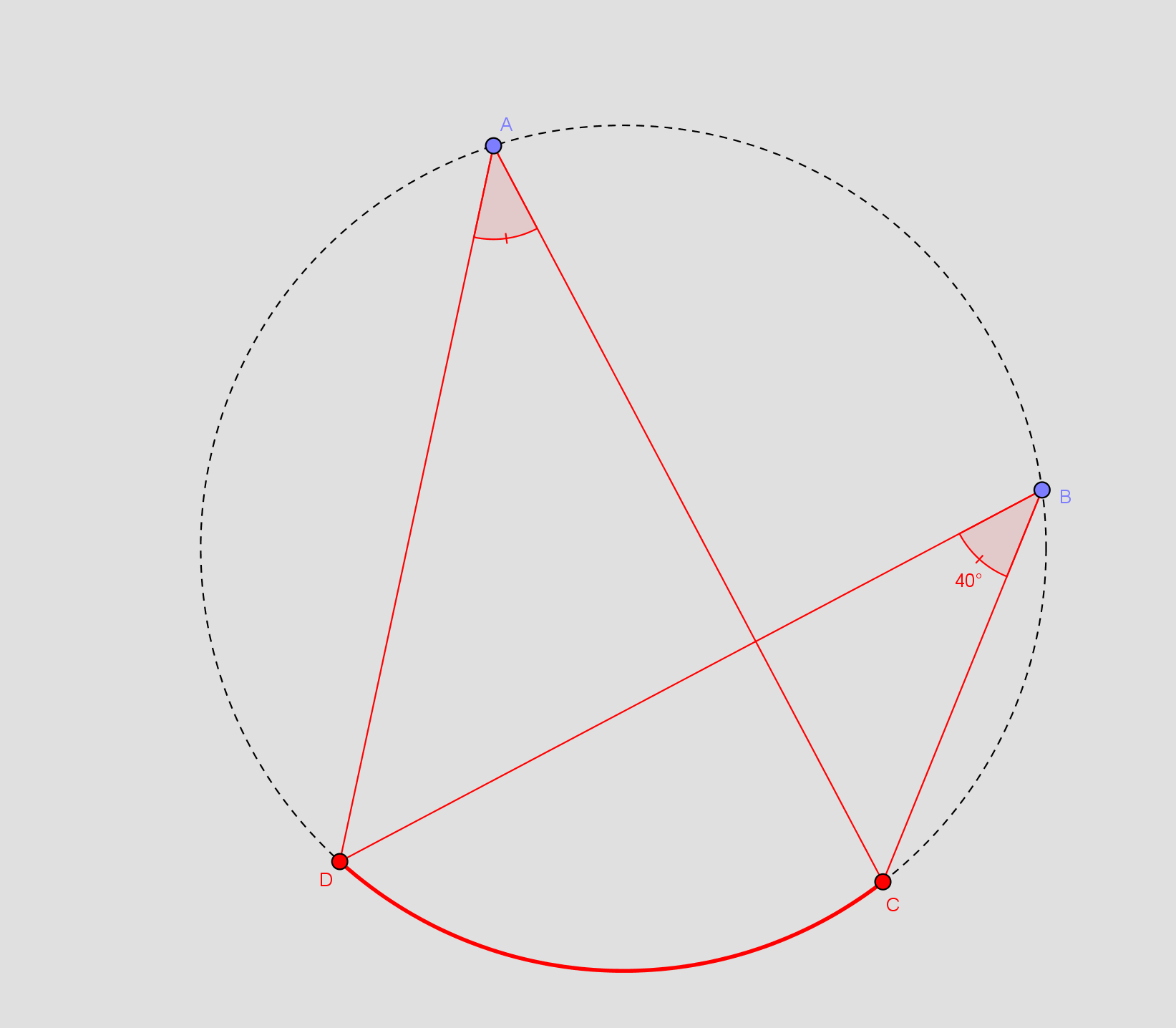
Vinkel CAD spænder over buen CD. Det gør vinkel CBD også Derfor er de to vinkler lige store.
Svar #6
19. september 2021 af ringstedLC
De resterende vinkler kan bestemmes på samme måde som #4 angiver.
Svar #8
20. september 2021 af ca10
Når jeg følger de tip der er blevet givet kommer jeg frem til:.
Da CAD Spænder over buen og CD gør det samme, og de to vinkler er lige store. Vinkel DBC er er 400 så er vinklen i CAD også 400. De er perifervinkler over samme bue.
Så er vinkel A = 300 + 400 = 700
Vinklen I trekanten ADX (X er skæringspunket mellem AC og BD der danner fire rette vinkler så X = 900 )
D : 1800 - ( 900 + 400 ) = 500
Nu mangler der at bestemme de resterende vinkler i vinkel D og vinkel C i trekanten DCB som ses i den vehæftede fil
Trekant CAB spænder over buen CB og CDB spænder over den samme bue som er 300
så den resterende vinkel i D er 300
Så vinkel D er 500 + 300 = 800
Så den resterende vinkel V i vinkel C bliver V = 1800 - ( 300 + 400 +500 ) = 600 ,
Så vinkel C er 500 + 600 = 1100
Tak for svarene
Svar #10
20. september 2021 af ringstedLC
Der er fire par periferivinkler, der tilsammen dækker hele periferien. I hvert par er én af vinklerne opgivet. Den anden kan altså direkte bestemmes.
Flere vinkler i samme toppunkt benævnes ved punkterne på deres vinkelben. Og gerne i alfabetisk rækkefølge, dog således at toppunktet står i mellem de to andre.
Svar #12
21. september 2021 af ca10
Ud fra oplysningerne er givet:
For det første:
Der er fire par perifervinkler, der tilsammen dækker hele periferien. I hvert par er én af vinklerne opgivet. Den anden kan altså direkte bestemmes.
For det andet:
Vinkel CAD spænder over buen CD. Det gør vinkel CBD også Derfor er de to vinkler lige store.
Så vinkel CBD = 400 ,
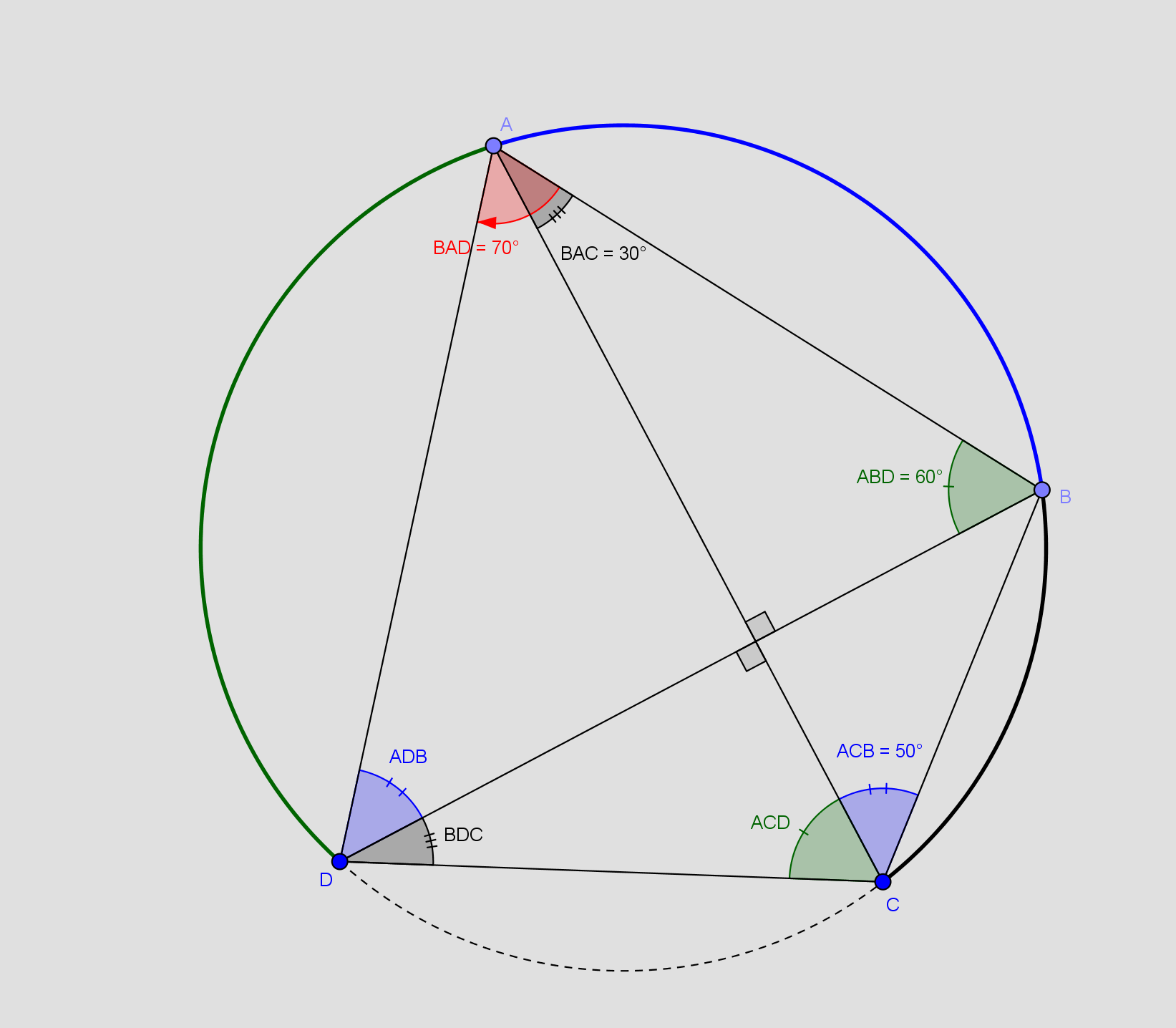
Vinkel A = BAD = CBD + BAC = 400 + 300 = 700
Vinkel B = 600 + 400 = 1000
Vinkel ACD spænder over buen AD. Det gør ABD også derfor er de to vinkler lige store
Vinkel ABD = 600
Vinkel C = ACB + ABD = 500 + 600 = 1100
Vinkel ADB spænder over buen AB. Det samme gør ACB også derfor er de to vinkler lige store
Vinkel ACB = 500
Vinkel BDC spænder over buen BC. Det samme gør BAC også derfor er de to vinkler lige store
Vinkel D = ACB + BAC = 500 + 300 = 800
Svar #13
21. september 2021 af ringstedLC
Nydelig opstilling, dog smutter det i de to sidste linjer.
Desværre bruges argumenterne til at konkludere nogle af de opgivne vinklers værdi og ikke de ubekendtes.
- Sammenlign figurerne i #5 og #9 med opgavens figur.
- Der er 4 + 4 ubekendte periferivinkler.
- Og glem nu ikke de rette vinkler.
PS. "Det samme gør (vinkel) ACB også..." eller "Det samme gør (vinkel) ACB også". Ellers giver "samme" og "også" dobbeltkonfekt.
Svar #14
21. september 2021 af ca10
Tak for svaret.
Det er en svær opgave og jeg vil gå min løsning på opgave på 9098 igennem i én gang til og ser på, hvad det er der er gået galt, når det smutter i de to sidste linjer.
Svar #15
22. september 2021 af ca10
Jeg har gået opgaven igennem og prøver at løse således:
Ved at bestemme de fire perifervinkler og anvende rette vinkler og viden om at vinkelsummen i en trekant altid er 1800 og de vinkler der direkte er oplyst, har jeg forsøgt at bestemme vinklerne på figuren således:
CAD spænder over buen CD, det gør Vinkel CBD også, B = 400 så A = 400
Vinkel A = BAD = BAC + CBD = 300 + 400 = 700
Vinkel B = 600 + 400 = 1000
ACD spænder over buen AD. det gør ABD også, så i ABD er B = 600 så i ACD er C = 600 og i ACB er C = 500
Vinkel C = ABD + ACB = 600 + 500 = 1100
Vinkel D kan bestemmes på to måder:
1) I en trekant vinkelsummen altid er 1800 .
Vinklerne ACD og CAD er henholdsvis A = 400 og C = 600
Vinkel D = 1800 - ( CAD + ACD ) = 1800 - ( 400 + 600) = 1800 - 1000 = 800
2)
ADB spænder over buen AB, og ACB spænder over buen AB, I ACB hvor C = 500 så i ADB er D = 500
BDC spænder over buen BC og BAC spænder over buen BC. I BAC hvor A = 300 så i BDC er D = 300
Vinkel D = ADB + BDC = 500 + 300 = 800
Jeg håber nu at alle vinklerne på figuren, er blevet bestemt rigtigt.
Skriv et svar til: Vinkler i figuren, Ny Zigma, Opgave 9 098, Side 247 (Henry Schultz med flere)
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.