Matematik

integralregning

14. oktober 2021 af freja9292 - Niveau: A-niveau

En funktion ff er givet ved f(x)=−x²+5
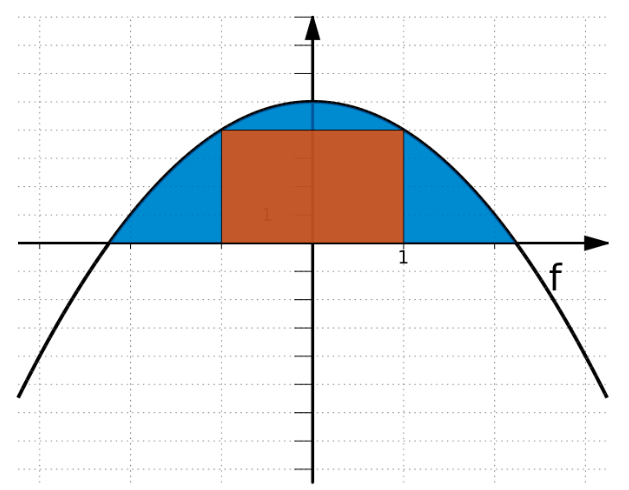
Grafen for funktionen afgrænser sammen med førsteaksen et område, hvor et rektangel er udskåret. Rektanglet skærer grafen for f ved funktionsværdien 4. Hvad er arealet af det blå område på figuren?(se fil)

har ingen ide om, hvordan jeg regner dette ud

Vedhæftet fil: Skærmbillede 2021-10-14 kl. 19.23.39.png

Brugbart svar (1)

Svar #1
14. oktober 2021 af JimmyMcGill

Brugbart svar (2)

Svar #2
14. oktober 2021 af JimmyMcGill

Først har du det brune område. Du ved ud fra oplysningerne, at højden af rektanglet er 4, samt at bredden af rektanglet er 2. (Den går jo fra -1 til 1). Du regner arealet af rektanglet ved

$A_{\text{rektangel}}=h\cdot b$ hvor $h=4$ og $b=2.$

Dernæst løser du ligningen $f(x)=0$ for at finde integrationsgrænserne. Jeg får $f(x)=0\Leftrightarrow x=\pm \sqrt{5}$ , derfor er mine integrationsgrænser $a=-\sqrt{5}$ og $b=\sqrt{5}$ .

Arealet under grafen er $A_{\text{under graf}}=\int_{-\sqrt{5}}^{\sqrt{5}}(-x^2+5)dx$

Arealet af det blå område er $A_{\text{bl\aa}}=A_{\text{under graf}}-A_{\text{rektangel}}$ . Får du følgende svar?

$A_{\text{bl\aa}}=\frac{20\sqrt{5}}{3} - 8\approx 6.907$

Brugbart svar (1)

Svar #3
14. oktober 2021 af ringstedLC

$\begin{align*} A_{blaa}+A_{rekt} &= \int_{r_1}^{r_2}\!f(x)\,\mathrm{d}x \end{align*}$

Skriv et svar til: integralregning

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.