Matematik

Skaler to vektorer

23. november 2021 af javannah5 - Niveau: A-niveau

Nogen der ved hvordan man løser 3’en?

Vedhæftet fil: B28CA4E2-34F2-4AC3-B47B-B46BC56FEADA.jpeg

Brugbart svar (0)

Svar #1
23. november 2021 af PeterValberg

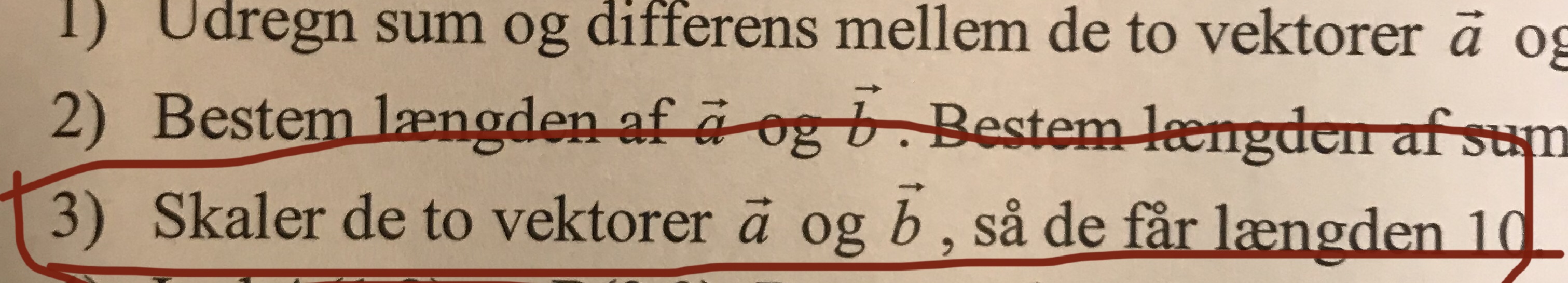
Du skalerer en vektor ved at forlænge dets koordinater med det samme tal

$s\cdot\vec{v}=s\cdot\binom{a}{b}=\binom{s\cdot a}{s\cdot b}$

du skal altså finde en skalar, der får vektorernes længde til at være 10
Du kan bestemme længden af en vektor vha. pythagoras

$\left | \vec{v}\right |=\left | \binom{a}{b} \right |=\sqrt{a^2+b^2}$

- - -

mvh.

Peter Valberg
(YouTube)

Brugbart svar (0)

Svar #2
23. november 2021 af PeterValberg

Du kan også benytte, at prikproduktet af en vektor med sig selv
er lig med kvadratet på vektorens længde

$\vec{a}\cdot\vec{a}=\left |\vec{a}\right |^2$

hvilket jo betyder, at du skal løse:

$\binom{s\cdot a}{s\cdot a}\cdot\binom{s\cdot a}{s\cdot a}=10^2$

mht. s

tilsvarende for vektor b

- - -

mvh.

Peter Valberg
(YouTube)

Brugbart svar (0)

Svar #3
23. november 2021 af PeterValberg

Vedr. #2

En lille tastefejl, jeg mener selvfølgelig

$\binom{s\cdot a_1}{s\cdot a_2}\cdot \binom{s\cdot a_1}{s\cdot a_2}=10^2$

hvor s er den søgte skalar og a₁og a₂ er vektorens koordinater

- - -

mvh.

Peter Valberg
(YouTube)

Svar #4
23. november 2021 af javannah5

hvad er meningen der skal stå på s plads?

Brugbart svar (0)

Svar #5
23. november 2021 af ringstedLC

#4: Det kommer da an på vektorens koordinater.

Brugbart svar (0)

Svar #6
24. november 2021 af PeterValberg

#4 s er den, i følge opgaveteksten, søgte skalar, der får længden
af hhv. vektor a og vektor b til at blive lig med 10... det er DEN,
du skal bestemme ved at indsætte de kendte vektorkoordinater og løse ligningen

- - -

mvh.

Peter Valberg
(YouTube)

Svar #7
26. november 2021 af javannah5

Kan du sende mig en video, der forklarer det?

Brugbart svar (0)

Svar #8
26. november 2021 af PeterValberg

#7 Nej, det kan jeg desværre ikke, men du har:

$\binom{s\cdot a_1}{s\cdot a_2}\cdot \binom{s\cdot a_1}{s\cdot a_2}=10^2$

$sa_1\cdot sa_1+sa_2\cdot sa_2=100$

$s^2(a_1^2+a_2^2)=100$

$s^2=\frac{100}{(a_1^2+a_2^2)}$

$s=\pm\sqrt{\frac{100}{(a_1^2+a_2^2)}}$

a₁ og a₂ er vektor a^'s oprindelige koordinater (tilsvarende for vektor b)

- - -

mvh.

Peter Valberg
(YouTube)

Skriv et svar til: Skaler to vektorer

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.