Matematik
Bestem a og b - optimering
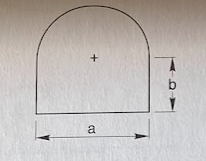
I forbindelse med en bygningsrenovering skal der udformes et vindue som vist på den vedhæftede figur.
Vinduets omkreds er 5 m, og målene er a skal fastlægges ud fra ønsket om, at der skal komme størst mulig lysmængde gennem vinduet
bestem ud fra de nævnte forudsætninger a og b.
Nogle der kan hjælpe?
Svar #1
24. marts 2022 af Christianfslag
Prøv at følg nedenstående punkter. Hvis du stadig har problemer eller forundringer, så skriv igen.
Trin 1 - Identificér problemet (det der skal optimiseres)
Trin 2 - Tegn en skitse
Trin 3 - Opskriv optimiseringen som funktion af de variable
Trin 4 - Reducér til én variabel ved at beskrive de(n) andre/anden
Trin 5 - Find kritiske punkter
- Differentier den opskrevne funktion
- Find f'(x)=0
Trin 6 - Validér kritisk punkt
Er den fundne værdi gældende for eventuelle begrænsninger af domænet for den variable?
Svar #2
25. marts 2022 af Anonym706
Hej igen.
Optimisering er et nyt emne for mig, og er derofr ret usikker i udførelsen af dette. Er det muligt du kan forklare fra trin 3?
Svar #4
26. marts 2022 af ringstedLC
Trin 1: Maksimalt areal giver størst mulig lysmængde.
Jeg ville bytte om på trin 3 og 4.
Trin 3: Du skal danne en funktion af én de to variable, der giver arealet og bestemme den værdi af variablen, der giver maksimum af funktionen. Bestem først et udtryk for den ene variable fx b:
Trin 4: Vinduets areal kan nu beskrives som en funktion kun af a:
Trin 5:
Skriv et svar til: Bestem a og b - optimering
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.