Matematik
Opgave matematik hjælp
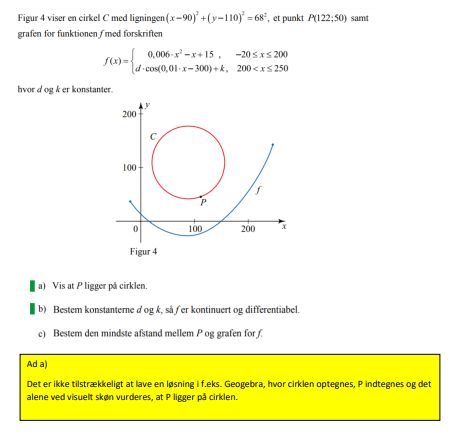
Hej allesammen, er der nogle der kan hjælpe mig med denne opgave? har siddet med den. Men forstår ikke helt hvilken formler og hvordan jeg skal løse den? tak på forhånd:) Se vedhæftet
Svar #6
09. august 2022 af Eksperimentalfysikeren
mathon: Noget er gået galt med dit svar. Jeg kan kun se formatteringskoder og tekststumper: "\small \small..."
Da jeg sendte ovenstående, kom den korrekt formatterede tekst frem. Mystisk!
Svar #8
10. august 2022 af mathon
Når vinklen mellem den lodrette afstandslinje og den vinkelrette afstandslinje er
har man
da tillige er hældningsvinklen for tangenten i det søgte punkt
.
Da er spids:
Der defineres
på TInspire:
Da vektorerne
haves:
Svar #9
10. august 2022 af Capion1
c)
Mindste afstand mellem P og grafen for f for x ≤ 200 er
minimum af udtrykket = 56,1956... for x = 160,0651...
Svar #18
14. august 2022 af ringstedLC
#15: Du skal bestemme to ubekendte så funktionen er differentiabel. Det kræver, at der opstilles og løses to ligninger med to ubekendte.
En funktion er differentiabel, når den er kontinuert (sammenhængende) og ikke har nogen "knæk".
Ved løsning af den første ligning i #7 sikres det, at grafen ikke har nogen "knæk", da de to dele får samme diff.-kvotient for x = 200:
- Indsæt x = 200
- Differentiér på begge sider.
- Bestem d.
Ved løsning af den anden ligning i #7 sikres det, at grafen er kontinuert for x = 200:
- Indsæt x = 200 og d
- Bestem k.
NB: Opdatér din profil mht. uddannelse!
Svar #20
17. august 2022 af lingling2200
Ved du hvorfor jeg ikke får samme b værdi som jer?