Hældningsfelter

Hej. Ud fra hældningsfelternes retning kan vi se, at løsningerne til differentialligningen er aftagende eksponentielle funktioner. Idet h(x) = 4e^0,3x er en voksende funktion(fortegnet på eksponenten er positiv), så kan vi argumentére for, at h ikke kan være en løsning til differentialligningen.

Men de to andre er da også voksende funktioner når e^-0.3 er et positivt tal?

Ligemeget hvilken x-værdi jeg stopper ind i de andre to funktioner, får jeg også et positivt tal

#2: At funktionsværdier er positive gør ikke en funktion voksende.

Men hvis x er et negativt tal, så er eksponenten jo også negativ?

Hej igen. e^x > 0 for alle værdier af x. 

e^x er altid større end nul og kan derfor ikke være negativ:)) Men grafen for e^-x er aftagende, mens grafen for e^x er voksende.

Jeg tænkte nemlig hvis x er negativ, så er hele eksponenten negativ da 0.3 gange et negativt tal er en negativ eksponent?

#5

Kan godt forstå hvad du mener. For e^x gælder dog at x ikke kan være negativ, idet værdimængden for e^x kun er alle positive reelle tal:)

#7

Det er helt korrekt at et negativt x ganget på en positiv koefficient ville gøre, at hele eksponenten er negativ. Men da e^x ikke afbilder negative x-værdier, er den eneste måde eksponenten kan være negativ på, hvis koefficienten der er ganget på x'et er negativ:) Håber det giver mening. (Grafen for en eksponentiel fkt. vil altid ligge over x-aksen, uanset om den er voksende eller aftagende)

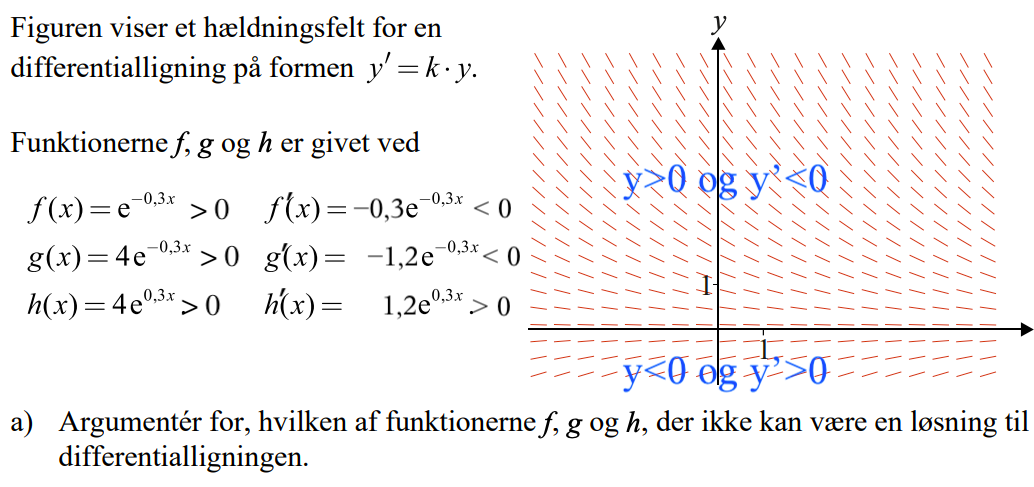
#0. Hældningsfeltet kan deles i to dele (se venligst nedenstående billede):

1) y > 0 (linjeelementerne er over x-aksen) og y' < 0 (alle linjeelementer har negativ hældning).

2) y > 0 (linjeelementerne er under x-aksen) og y' > 0 (alle linjeelementer har positiv hældning).

En løsning skal enten opfylde 1), 2) eller y = 0, der er et specialtilfælde. Funktionerne f og g opfylder 1), mens h ikke opfylder nogen af kravene. Derfor kan h ikke være en løsning til differentialligningen. 

#9

Det er helt korrekt at et negativt x ganget på en positiv koefficient ville gøre, at hele eksponenten er negativ. Men da e^x ikke afbilder negative x-værdier, er ...

I så fald afbilder de afledte heller ikke negative x-værdier og kan derfor ikke give det hældningsfelt...

" e^x " er defineret for alle værdier af x.

#9

#7

Det er helt korrekt at et negativt x ganget på en positiv koefficient ville gøre, at hele eksponenten er negativ. Men da e^x ikke afbilder negative x-værdier, er den eneste måde eksponenten kan være negativ på, hvis koefficienten der er ganget på x'et er negativ:) Håber det giver mening. (Grafen for en eksponentiel fkt. vil altid ligge over x-aksen, uanset om den er voksende eller aftagende)

Det er måske brugbart at overveje, hvorfor det gælder, at exp(x)>0, for alle x. Det er ikke trivielt for alle. En nem måde at indse det på er:

Antag, at der eksisterer et x i de reelle tal, således exp(x)=0. Da vil der for dette x gælde, at for alle a i de reelle tal, så er exp(x)*a=0. Lad et sådant tal, a, være exp(-x). Da har vi, at exp(x)*exp(-x)=exp(x-x)=exp(0)=1 /= 0. Dermed har vi en modstrid, hvorfor exp(x) må være forskellig for 0 for alle x.

Videre har vi så, at exp(0)=1, samtidig med, at exp(x) er kontinuert, hvormed mellemværdisætningen giver, at exp(x)>0 for alle x, da der ellers havde eksisteret x, således exp(x)=0, hvilket, vi har vist, ikke er tilfældet.

Som en anden gør opmærksom på, så er exp(x) en afbildning fra de reelle tal ind i den positive reelle akse; i hvert fald i dette tilfælde.

#12

Mange tak til Jer begge to. Kan godt se det :)

Ved ikke lige hvad jeg har lavet den dag, det er pinligt, for det er da godt nok ren vrøvl det jeg skrev. Det går godt nok ikke, at jeg skriver noget så forkert herinde, hvor folk forhåbentlig skal få en bedre forståelse, og ikke bare blive mere forvirrede. For det er selvfølgelig, som I også skriver en afbildning, der afbilder de reelle tal ind i den positive reelle akse. 

Jeg opdagede godt selv, at det var helt galt det jeg havde skrevet, men kunne ikke slette eller redigere opslaget igen.

Du har 10 min. til at redigere dit indslag. Herefter kan opslaget kun slettes af SP.

Alternativ: Brug "Citér", marker det forkerte og skriv eventuelt det rigtige under citér-feltet.