Matematik

Geometrisk fortolkning

05. marts kl. 20:07 af cecilie1606 - Niveau: A-niveau

Hej

Jeg har beregnet følgende integraler, og skal lave en geometrisk fortolkning af resultaterne.

Dette har jeg aldrig gjort før. Hvordan gør jeg det.

(se de to vedhæftede filer, for opgaverne og resultaterne)

Vedhæftet fil: Opgave 16.png

Svar #1
05. marts kl. 20:07 af cecilie1606

Resultater:

Vedhæftet fil:Opgaver.png

Brugbart svar (0)

Svar #2
05. marts kl. 20:36 af ringstedLC

Brugbart svar (0)

Svar #3
05. marts kl. 20:36 af ringstedLC

$\begin{align*} \tfrac{4}{3}-\left ( -\tfrac{1}{3}+1\cdot (-1) \right ) &= \tfrac{4}{3}-\left (-\tfrac{4}{3} \right )\;{\color{Red} \neq }\;0 \end{align*}$

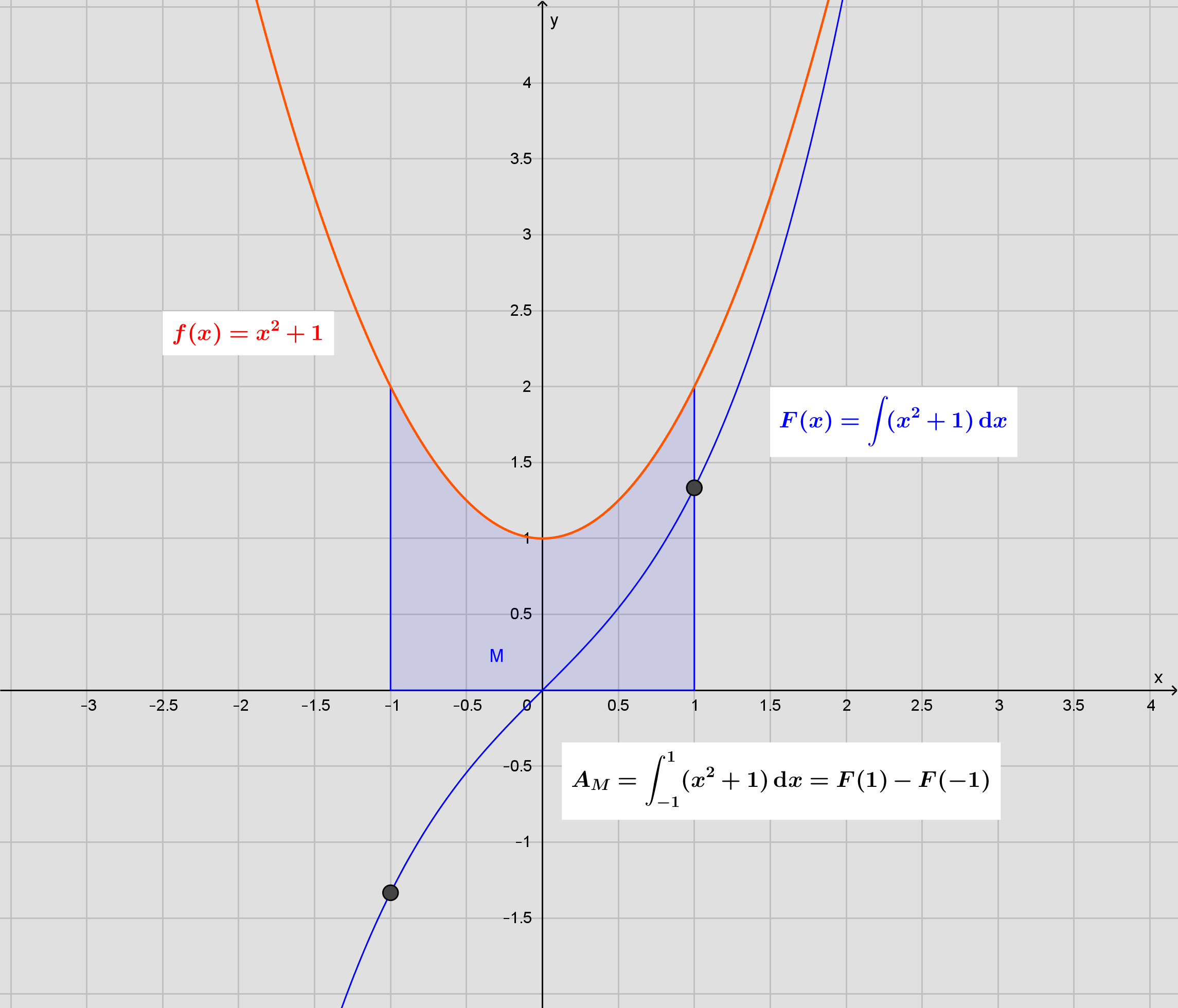
Fortolkning: Integranden f(x) er en "glad parabel med toppunkt i (0, 1). Det bestemte integrale er arealet mellem grafen og x-aksen.

4. Gør prøve:

$\begin{align*} \left (-2x^3+x\right )' &\;{\color{Red} \neq }\;-3x+1 \end{align*}$

Svar #4
05. marts kl. 21:34 af cecilie1606

Okay, men hvordan kommer du frem til fortolkningen?

Er stadig ikke med på hvor man "ser" fortolkningen henne?

Brugbart svar (0)

Svar #5
05. marts kl. 22:31 af ringstedLC

Vedhæftet fil:_0.png

Brugbart svar (0)

Svar #6
06. marts kl. 11:41 af AMelev

#0 Hvis f(x) er kontinuert i et interval [a,b] og positiv i ]a,b[, er $\int_{a}^{b}f(x)dx$ arealet af den punktmængde, der lodret er begrænset af f-grafen og x-aksen og vandret af linjerne x = a og x = b.
På "matematisk": $\int_{a}^{b}f(x)dx=Areal(\begin{Bmatrix} (x,y)|a\leq x\leq y \wedge 0\leq y\leq f(x) \end{Bmatrix})$

Du skal altså tjekke, at de pågældende funktioner opfylder betingelserne, og hvis de gør det, kan du "oversætte" integralet til arealet af den aktuelle punktmængde.

Skriv et svar til: Geometrisk fortolkning

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.