Matematik

projekt: kunstig sø HJÆLP

04. maj kl. 15:35 af fuckmath - Niveau: B-niveau

hej, vi er to piger som gerne vil have hjælp til at komme i gang med vores matematik projektopgave. her er opgaven:

Billedet viser en kunstig sø i udkanten af en by. Søen er ca. 2,5 km lang og i gennemsnit 240 meter bred.

Der skal ses på beregninger vedrørende søens geometri samt koncentrationen af fosfor.

f(x) = 0,046582x² - 0,1285x + 0,35

g(x) = 0,14727x² - 0,3451x + 0,20

Funktionen b har forskriften

b(x) = 0,5 * sin(-0,02x + 1,6) + 0,5 x ∈ [0; 240]

Funktionen v har forskriften

v(x) = 1,5 x ∈ [0; 240]

Middeldybden af søen kan bestemmes som middelværdien af dette tværsnit af søen. Middelværdien kan bestemmes som

Miljøstyrelsen anbefaler en maksimumsgrænse for koncentration af fosfor på 0,05-0,10 kg/m3. Der er 280.000 kg fosfor i søen.

1. Bestem den største og den mindste bredde af søen.
2. Bestem overfladearealet af søen.
3. Bestem den største og mindste dybde i søen med udgangspunkt i dette tværsnit.
4. Bestem middeldybden.
5. Undersøg, om koncentrationen af fosfor i søen overholder Miljøstyrelsens anbefalinger.

please hjælp os :)

Brugbart svar (0)

Svar #1
04. maj kl. 19:13 af MentorMath

Hej Fuckmath

Jeg er med på, at funktionerne f og g må angive noget som en funktion af søens længde, mens funktionerne b og v må angive noget som en funktion af søens bredde. Er der givet hvad værdierne på y-aksen for henholdsvis f, g og b, v angiver? Det virker lidt som om, der mangler noget information..

"Billedet viser en kunstig sø i udkanten".. Er det eventuelt muligt, at i kan vedhæfte billedet også?

Brugbart svar (0)

Svar #2
05. maj kl. 01:14 af SuneChr

1) Søens bredde er ( f(x) - g(x) )
     Bestem min og maks af ( f(x) - g(x) ) indenfor definitionsmængden.
2) Integrér   ( f(x) - g(x) )  indenfor definitionsmængden.
3) Find min og maks af b(x) ved differentiation af b(x) .
4) Integrationsformlen for middeltallet.
5) Søens rumfang: overfladen gange middeldybden. Overholder indholdet af phosphor anbefalingen?

Svar #3
05. maj kl. 10:38 af fuckmath

#1
Hej Fuckmath

Jeg er med på, at funktionerne f og g må angive noget som en funktion af søens længde, mens funktionerne b og v må angive noget som en funktion af søens bredde. Er der givet hvad værdierne på y-aksen for henholdsvis f, g og b, v angiver? Det virker lidt som om, der mangler noget information..

"Billedet viser en kunstig sø i udkanten".. Er det eventuelt muligt, at i kan vedhæfte billedet også?

Svar #4
05. maj kl. 11:25 af fuckmath

#0
hej, vi er to piger som gerne vil have hjælp til at komme i gang med vores matematik projektopgave. her er opgaven:

Billedet viser en kunstig sø i udkanten af en by. Søen er ca. 2,5 km lang og i gennemsnit 240 meter bred.

Der skal ses på beregninger vedrørende søens geometri samt koncentrationen af fosfor.

f(x) = 0,046582x² - 0,1285x + 0,35

g(x) = 0,14727x² - 0,3451x + 0,20

Funktionen b har forskriften

b(x) = 0,5 * sin(-0,02x + 1,6) + 0,5 x ∈ [0; 240]

Funktionen v har forskriften

v(x) = 1,5 x ∈ [0; 240]

Middeldybden af søen kan bestemmes som middelværdien af dette tværsnit af søen. Middelværdien kan bestemmes som

Miljøstyrelsen anbefaler en maksimumsgrænse for koncentration af fosfor på 0,05-0,10 kg/m3. Der er 280.000 kg fosfor i søen.

1. Bestem den største og den mindste bredde af søen.
2. Bestem overfladearealet af søen.
3. Bestem den største og mindste dybde i søen med udgangspunkt i dette tværsnit.
4. Bestem middeldybden.
5. Undersøg, om koncentrationen af fosfor i søen overholder Miljøstyrelsens anbefalinger.

please hjælp os :)

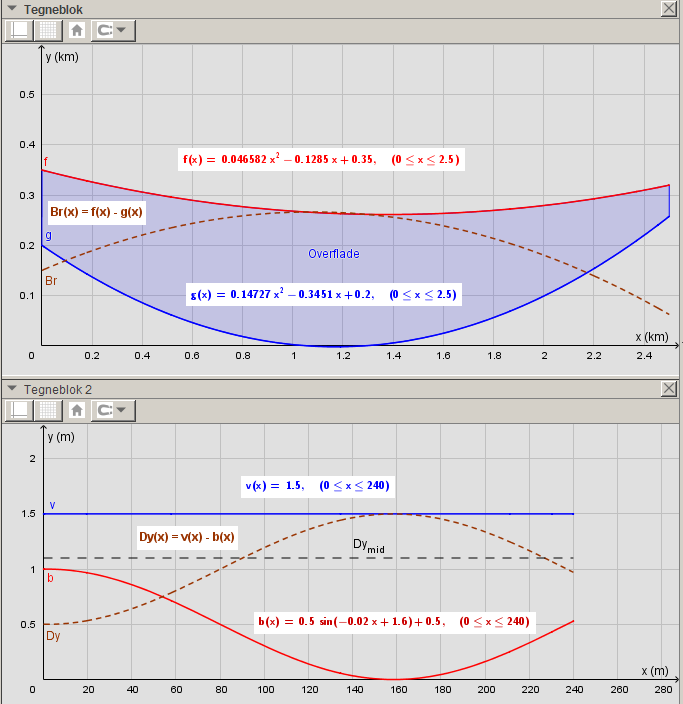
første billede = viser en tegning af søen set i plan. Kanterne af søen kan tilnærmelsesvis angives ved graferne for funktionerne [f] og [g] , der har forskrifterne

andet billede = viser et repræsentativt tværsnit i søen. Vandoverfladen ligger på grafen for funktionen v, og bunden beskrives ved grafen for funktionen b. Målene her er i meter.

Brugbart svar (0)

Svar #5
06. maj kl. 11:47 af ringstedLC

Vedhæftet fil:ScreenShot_20230505192618.png

Brugbart svar (0)

Svar #6
06. maj kl. 11:48 af ringstedLC

1. Se "Tegneblok" på figuren:

$\begin{align*} Br(x) &= f(x)-g(x) \\Br'(x)=0 &= (...)\Rightarrow x=x_0 \\ Br_{maks} &= Br(x_0)=...\;(\textup{km}) \\ Br_{min} &= Br(2.5)=...\;(\textup{km}) \end{align*}$

$\begin{align*} A &= \int_{0}^{2.5}\!\bigl(f(x)-g(x)\bigr)\,\mathrm{d}x= ...\;(\textup{km}^2) \end{align*}$

Brugbart svar (0)

Svar #7
06. maj kl. 11:48 af ringstedLC

3. Se "Tegneblok 2":

$\begin{align*} Dy(x) &= v(x)-b(x)\\ Dy_{maks} &= 1.5-b_{min} \\ Dy_{maks} &= 1.5-\bigl(0.5\cdot \textup{sinus}_{min}+0.5\bigr)=...\,(\textup{m}) \\\\ Dy_{min} &= 1.5-b_{maks} \\ Dy_{min} &= 1.5-\bigl(0.5\cdot \textup{sinus}_{maks}+0.5\bigr)=...\,(\textup{m}) \end{align*}$

Brugbart svar (0)

Svar #8
06. maj kl. 11:49 af ringstedLC

$\begin{align*} m &= \frac{1}{b-a}\int_{a}^{b}\!\bigl(v(x)-b(x)\bigr)\,\mathrm{d}x \\ Dy_{mid} &= \frac{1}{240}\int_{0}^{240}\!\bigl(1-0.5 \sin(-0.02x+1.6)\bigr)\,\mathrm{d}x=...\;(\textup{m}) \end{align*}$

Brugbart svar (0)

Svar #9
06. maj kl. 11:49 af ringstedLC

$\begin{align*} K &= \frac{280\cdot 10^3\,\textup{kg}}{A\cdot Dy_{mid}} \\ K&= \frac{280\cdot 10^3\,\textup{kg}}{A\cdot \textup{km}^{-2}\cdot \bigl(10^3\,\textup{m}\bigr)^2\cdot Dy_{mid}} =...\;\frac{\textup{kg}}{\textup{m}^3} \end{align*}$

Svar #10
06. maj kl. 15:16 af fuckmath

#6
1. Se "Tegneblok" på figuren:

$\begin{align*} Br(x) &= f(x)-g(x) \\Br'(x)=0 &= (...)\Rightarrow x=x_0 \\ Br_{maks} &= Br(x_0)=...\;(\textup{km}) \\ Br_{min} &= Br(2.5)=...\;(\textup{km}) \end{align*}$

2.

$\begin{align*} A &= \int_{0}^{2.5}\!\bigl(f(x)-g(x)\bigr)\,\mathrm{d}x= ...\;(\textup{km}^2) \end{align*}$

jeg forstår ikke helt hvordan jeg skal lave opgave 1. kunne du forklare hvordan jeg skal løse det?

Brugbart svar (0)

Svar #11
06. maj kl. 17:11 af ringstedLC

- Træk funktionen g fra funktionen f. Den forskel giver en tredje funktion Br som er en forskrift for bredden af søen.

- Dens maksimum (eller toppunkt) kan bestemmes ved at sætte dens diff.-kvotient lig med nul, løse ligningen og indsætte løsningen i funktionen.

- Minimumsbredden kræver nok ikke nærmere forklaring.

Svar #12
08. maj kl. 16:41 af fuckmath

#11
- Træk funktionen g fra funktionen f. Den forskel giver en tredje funktion Br som er en forskrift for bredden af søen.

- Dens maksimum (eller toppunkt) kan bestemmes ved at sætte dens diff.-kvotient lig med nul, løse ligningen og indsætte løsningen i funktionen.

- Minimumsbredden kræver nok ikke nærmere forklaring.

kan det passe at det giver følgende når jeg trækker funktionerne fra hinanden:

Br(x) = ∫-0,100688x²- 0,2166x + 0,15

og skal det nu differentieres eller integreres?

Brugbart svar (0)

Svar #13
08. maj kl. 19:13 af ringstedLC

#12 Både og.

Diff. giver maksimal bredde:

$\begin{align*} Br(x) &= f(x)-g(x) \\&= 0.046582x^2-0.1285x+0.35-\bigl(0.14727x^2-0.3451x+0.20\bigr) \\ &= 0.046582x^2-0.1285x+0.35-0.14727x^2\;{\color{Red} +}\;0.3451x-0.20 \\ Br(x) &= -0.100688x^2\;{\color{Red} +}\;0.2166x+0.15\;,\;0\leq x\leq 240\\ Br'(x)=0 &= (...)\Rightarrow x=x_0 \\ Br_{maks} &= Br(x_0)=...\;(\textup{km}) \\ Br_{min} &= Br(2.5)=...\;(\textup{km}) \end{align*}$

og det bestemte integrale giver søens overfladeareal.

$\begin{align*} A &= \int_{0}^{2.5}\!\bigl(f(x)-g(x)\bigr)\,\mathrm{d}x \\A &= \int_{0}^{2.5}\!Br(x)\,\mathrm{d}x= ...\;(\textup{km}^2) \end{align*}$

Svar #14
08. maj kl. 20:31 af fuckmath

har

#13
#12 Både og.

Diff. giver maksimal bredde:

1.

$\begin{align*} Br(x) &= f(x)-g(x) \\&= 0.046582x^2-0.1285x+0.35-\bigl(0.14727x^2-0.3451x+0.20\bigr) \\ &= 0.046582x^2-0.1285x+0.35-0.14727x^2\;{\color{Red} +}\;0.3451x-0.20 \\ Br(x) &= -0.100688x^2\;{\color{Red} +}\;0.2166x+0.15\;,\;0\leq x\leq 240\\ Br'(x)=0 &= (...)\Rightarrow x=x_0 \\ Br_{maks} &= Br(x_0)=...\;(\textup{km}) \\ Br_{min} &= Br(2.5)=...\;(\textup{km}) \end{align*}$

og det bestemte integrale giver søens overfladeareal.

2.

$\begin{align*} A &= \int_{0}^{2.5}\!\bigl(f(x)-g(x)\bigr)\,\mathrm{d}x \\A &= \int_{0}^{2.5}\!Br(x)\,\mathrm{d}x= ...\;(\textup{km}^2) \end{align*}$

har jeg differentierede det rigtigt?

Br'(x)= -0,100688 * 2x + 0,2166

Brugbart svar (0)

Svar #15
08. maj kl. 20:44 af ringstedLC

Ja, du har differentieret korrekt!

Sæt Br '(x) = 0, løs ligningen, indsæt løsningen i Br(x) og bestem maks. bredde.

Svar #16
08. maj kl. 20:52 af fuckmath

#15
Ja, du har differentieret korrekt!

Sæt Br '(x) = 0, løs ligningen, indsæt løsningen i Br(x) og bestem maks. bredde.

0 = -0,100688 * 2x + 0,2166

<=>

-0,2166 = -0,201376x

<=>

-0,2166/-0,201376 = x

<=>

x = 1,0756

Så sætter jeg løsningewn ind i Br(x) og får

Br(1,0756) = -0,100688 * 1,0756² + 0,2166 * 1,0756 + 0,15

Br(1,0756) = 0,266

Har jeg gjort det rigtigt?

Brugbart svar (0)

Svar #17
08. maj kl. 20:56 af ringstedLC

Det ser rigtigt ud. Husk enheden i dit svar.

Svar #18
08. maj kl. 21:03 af fuckmath

Jeg prøver at finde minimal bredde

2,5 = -0,201376x + 0,2166

<=>

2,2834 = -0,201376x

<=>

2,2834/-0,201376 = x

<=>

x = -11,339

Så sætter jeg løsningen ind i Br(x) og får

Br(-11,339) = -0,100688 * (-11,339)^2 + 0,2166 * (-11,339) + 0,15

Br(-11,339) = -15,2517

Jeg tror ikke det er rigtigt, men jeg ved ikke hvad der er forkert?

Brugbart svar (0)

Svar #19
08. maj kl. 21:50 af ringstedLC

Se på figuren og så på din løsning. Du kan ikke indsætte x = -11.... Ergo er der den ikke rigtig.

Se igen på figuren og tænk over om ikke søen må være smallest i den østlige ende, hvor x er ...

Svar #20
08. maj kl. 21:59 af fuckmath

#13
#12 Både og.

Diff. giver maksimal bredde:

1.

$\begin{align*} Br(x) &= f(x)-g(x) \\&= 0.046582x^2-0.1285x+0.35-\bigl(0.14727x^2-0.3451x+0.20\bigr) \\ &= 0.046582x^2-0.1285x+0.35-0.14727x^2\;{\color{Red} +}\;0.3451x-0.20 \\ Br(x) &= -0.100688x^2\;{\color{Red} +}\;0.2166x+0.15\;,\;0\leq x\leq 240\\ Br'(x)=0 &= (...)\Rightarrow x=x_0 \\ Br_{maks} &= Br(x_0)=...\;(\textup{km}) \\ Br_{min} &= Br(2.5)=...\;(\textup{km}) \end{align*}$

og det bestemte integrale giver søens overfladeareal.

2.

$\begin{align*} A &= \int_{0}^{2.5}\!\bigl(f(x)-g(x)\bigr)\,\mathrm{d}x \\A &= \int_{0}^{2.5}\!Br(x)\,\mathrm{d}x= ...\;(\textup{km}^2) \end{align*}$

hvordan finder jeg det bestemte integral? er det her rigtigt?

A = ∫-0,100688x2 + 0,2166x + 0,15

<=>

[-1/3 * 0,100688x³ + 1/2 * 0,2166x²]

Forrige 1 2 Næste

Der er 21 svar til dette spørgsmål. Der vises 20 svar per side. Spørgsmålet kan besvares på den sidste side. Klik her for at gå til den sidste side.