Matematik

Stykkevis lineær funktion

15. september 2023 af Quarr - Niveau: B-niveau

Kan I hjælpe mig med begge spørgsmål?

På forhånd tak!

Vedhæftet fil: promille.PNG

Brugbart svar (0)

Svar #1
15. september 2023 af mathon

Brugbart svar (1)

Svar #2
15. september 2023 af mathon

$\small \small \begin{array}{llllll} \textbf{a)}\\& \textup{N\aa r middagen slutter:}&0.6\cdot x\\\\& \textup{P\aa \ 2 timer aftager promillen:}&0.2\cdot 2=0.4\\\\& \textup{0-promille:}&0.6\cdot x-0.4=0\qquad \textup{x er middagens varighed}\\\\&& x=\frac{0.4}{0.6}=\frac{2}{3}\;\mathrm{time }= 40\;\mathrm{minutter }\\\\& \textup{Tid fra start til 0-promille:}&\left (40\;\mathrm{min} \right )+\left (2\;\mathrm{timer} \right )=2\;\mathrm{timer}\; 40\;\mathrm{min} \end{array}$

Brugbart svar (1)

Svar #3
15. september 2023 af mathon

$\small \small \small \small \begin{array}{lllll} \textbf{b)}\\& \textup{Gaffelfunktion:}&f(x)=\left\{\begin{matrix} 0.6\cdot x&0\leq x\leq \frac{2}{3}\\0.4-0.2\cdot x& \frac{2}{3}< x\leq 2 \end{matrix}\right. \end{array}$

Svar #4
15. september 2023 af Quarr

Burde a) og b) ikke give noget andet?

- - -

Brugbart svar (1)

Svar #5
15. september 2023 af ringstedLC

$\begin{align*} f(x) &= \left\{\begin{matrix} &0.6x\qquad\qquad\qquad &,\;0\leq x\leq\frac{2}{3}\quad\;\; \\ &0.4-0.2\cdot \left (x-\frac{2}{3} \right ) &\,,\;\frac{2}{3}\leq x\leq 2+\frac{2}{3} \end{matrix}\right. \\x) &= \left\{\begin{matrix} &0.6x\qquad &\qquad\quad\;\;\;,\;0\leq x\leq\frac{2}{3}\quad\;\; \\ &{\color{Red} \frac{8}{15}}-0.2x &\qquad\qquad,\;\frac{2}{3}\leq x\leq 2{\color{Red} \,+\,\frac{2}{3}} \end{matrix}\right. \end{align*}$

Brugbart svar (1)

Svar #6
15. september 2023 af ringstedLC

#4: Promillen vokser 3 gange så hurtigt som den aftager. Når det tager 2 timer at komme af med den, må det tage 2/3 time at opnå den.

Brugbart svar (1)

Svar #7
15. september 2023 af Eksperimentalfysikeren

#4 Jo, der er regnet forkert. Det er middagen, der varer 2 timer, ikke perioden bagefter.

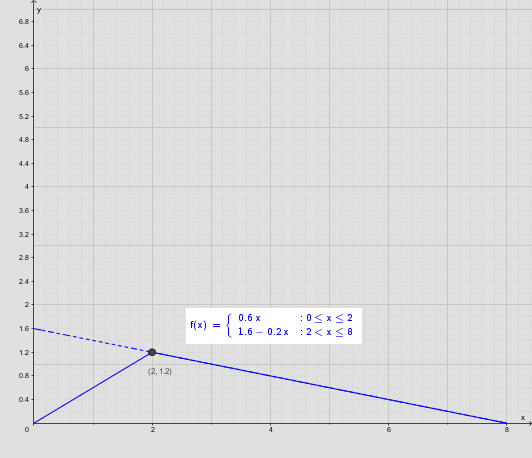
Middagen varer 2 timer og promillen vokser med 0,6 promille pr time, så hans promille er 1,2, når middagen slutter. Herefter falder promillen med 0,2 promille pr time. 1,2 promille/0,2 promille pr time = 6 timer. Ialt tager det 2 timers middag + 6 timers aftagen = 8 timer.

$f(x)=\left\{\begin{matrix} 0,6\cdot t & 0 \leq t\leq 2\\ 1,2-0,2\cdot t & 2< t\leq 8 \end{matrix}\right.$

Svar #8
16. september 2023 af Quarr

Det var også sådan jeg forstod det da jeg kiggede på opgaven. Derfor giver rigtig god mening, det du skriver. Mange tak for hjælpen!

- - -

Brugbart svar (1)

Svar #9
16. september 2023 af mathon

Sorry for fejllæsning:
.

$\small f(x)=\left\{\begin{matrix} 0,6\cdot t & 0 \leq t\leq 2\\ 1,2-0,2\cdot t & 2< t\leq \textbf{{\color{Red} 6}} \end{matrix}\right.$

Brugbart svar (1)

Svar #10
16. september 2023 af ringstedLC

Jeg læste heller ikke opgaven ordentligt, men fastholder dog:

$\begin{align*} f(x) &= \left\{\begin{matrix} &0.6x\qquad\qquad\quad\;\; &,\;0\leq x\leq 2\quad\;\;\, \\ &1.2-0.2\cdot \left (x{\color{Red} \,-\,2} \right ) &,\;2< x\leq 6+2 \end{matrix}\right. \\ f(x) &= \left\{\begin{matrix} &0.6x\qquad\qquad\quad\;\, &,\;0\leq x\leq 2\quad\;\;\, \\ &{\color{Red} 1.6}-0.2x \qquad\quad\, &,\;2< x\leq 8\quad\;\;\, \end{matrix}\right. \end{align*}$

Brugbart svar (1)

Svar #11
16. september 2023 af ringstedLC

Vedhæftet fil:_0.png

Brugbart svar (1)

Svar #12
19. september 2023 af mathon

Ja - tiden måles fra middagens start:

$\small \begin{array}{llllll} f(x) =\left\{\begin{matrix} 0.6x&0\leq x\leq 2\\ 1.6-0.2x&2< x\leq 8 \end{matrix}\right. \end{array}$

Svar #13
19. september 2023 af Quarr

Det er en uden hjælpemidler opgave.

#11 og #12

Hvorfor skal der stå 1,6 i stedet for 1,2 i den nederste forskrift?

- - -

Brugbart svar (1)

Svar #14
19. september 2023 af ringstedLC

En linje med hældningen a gennem punktet:

$\begin{align*}(x_1,y_1): y &= a\cdot \bigl(x-x_1\bigr)+y_1 &&\textup{formel (65)} \\ &= -0.2\cdot \bigl(x-2\bigr)+1.2 &&,\;x_1=2\;,\;y_1=0.6\cdot 2 \\ f(x) &= -0.2\,x+0.4+1.2 &&,\;2<x\leq 8 \end{align*}$

Skriv et svar til: Stykkevis lineær funktion

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.