Matematik

Matematik - Maksimums- og minimumsværdi (funktioner af 2 variable)

24. juni 2015 af xLaila (Slettet) - Niveau: Universitet/Videregående

Hej

Jeg har svært ved denne opgave i matematik:

Bestem maksimumværdi og minimumsværdi for funktionen:
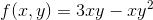
f(x,y)=3xy-xy^2

på mængden:

${(x,y) \epsilon \mathbb{R}|1\leq x\leq 2, 1\leq y\leq 2}$

Jeg har bestemt de kritiske (stationære) punkter til at være (0,0) og (0,3). Dog ligger disse punkter udenfor mængden. (skal de derfor ses bort fra?)

Jeg har også bestemt 4 randpunkter, som er:
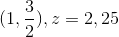
$(1,\frac{3}{2}), z=2,25$
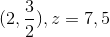
$(2,\frac{3}{2}), z=7,5$
(2,1), z=4
(2,2), z=4
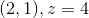
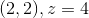
Jeg ved ikke om jeg har udført opgaven korrekt. Nogen som kan hjælpe? og hjælpe mig med at bestemme maksimumsværdien og minimumsværdien?

Brugbart svar (0)

Svar #1
24. juni 2015 af Soeffi

#0

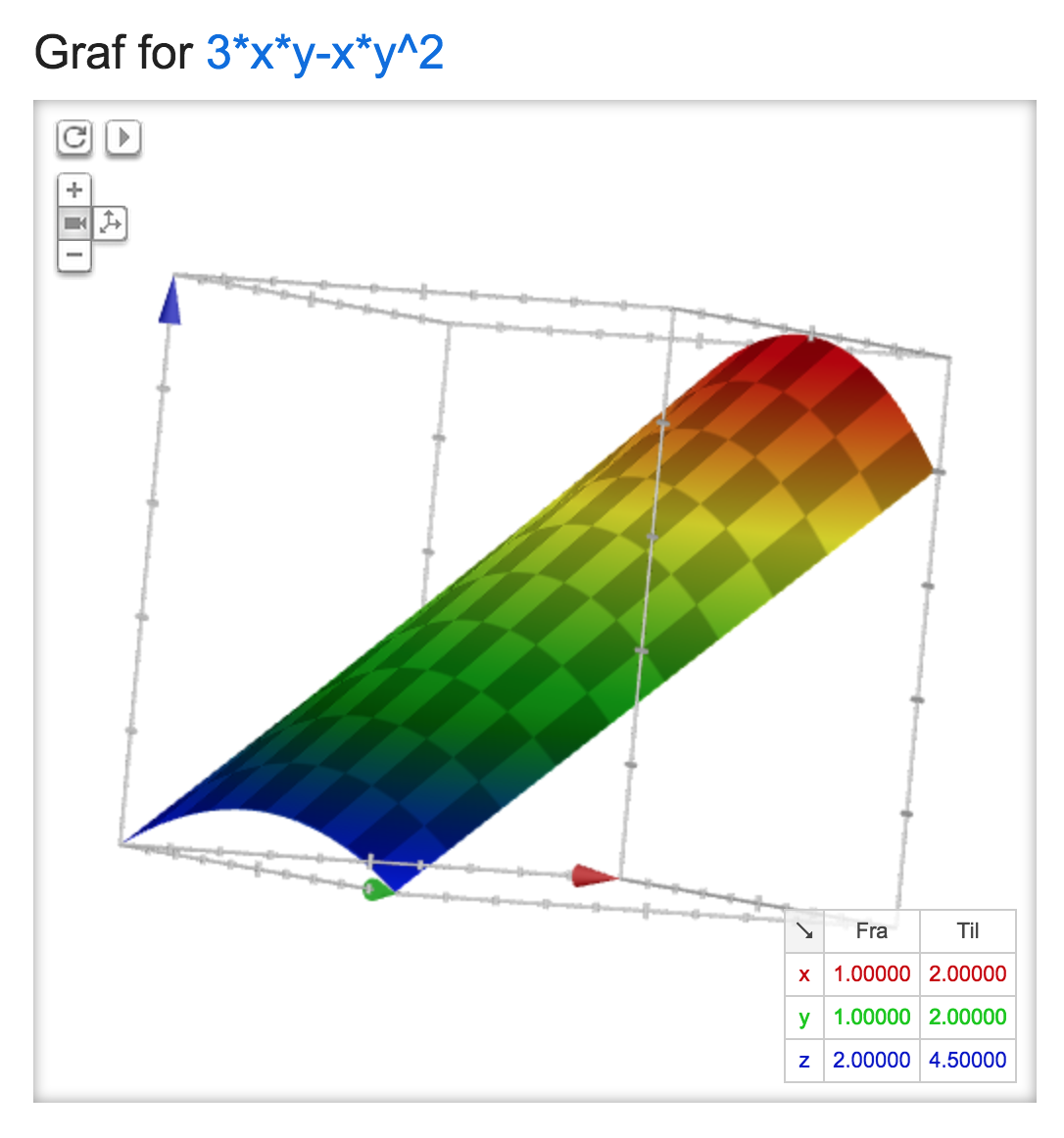
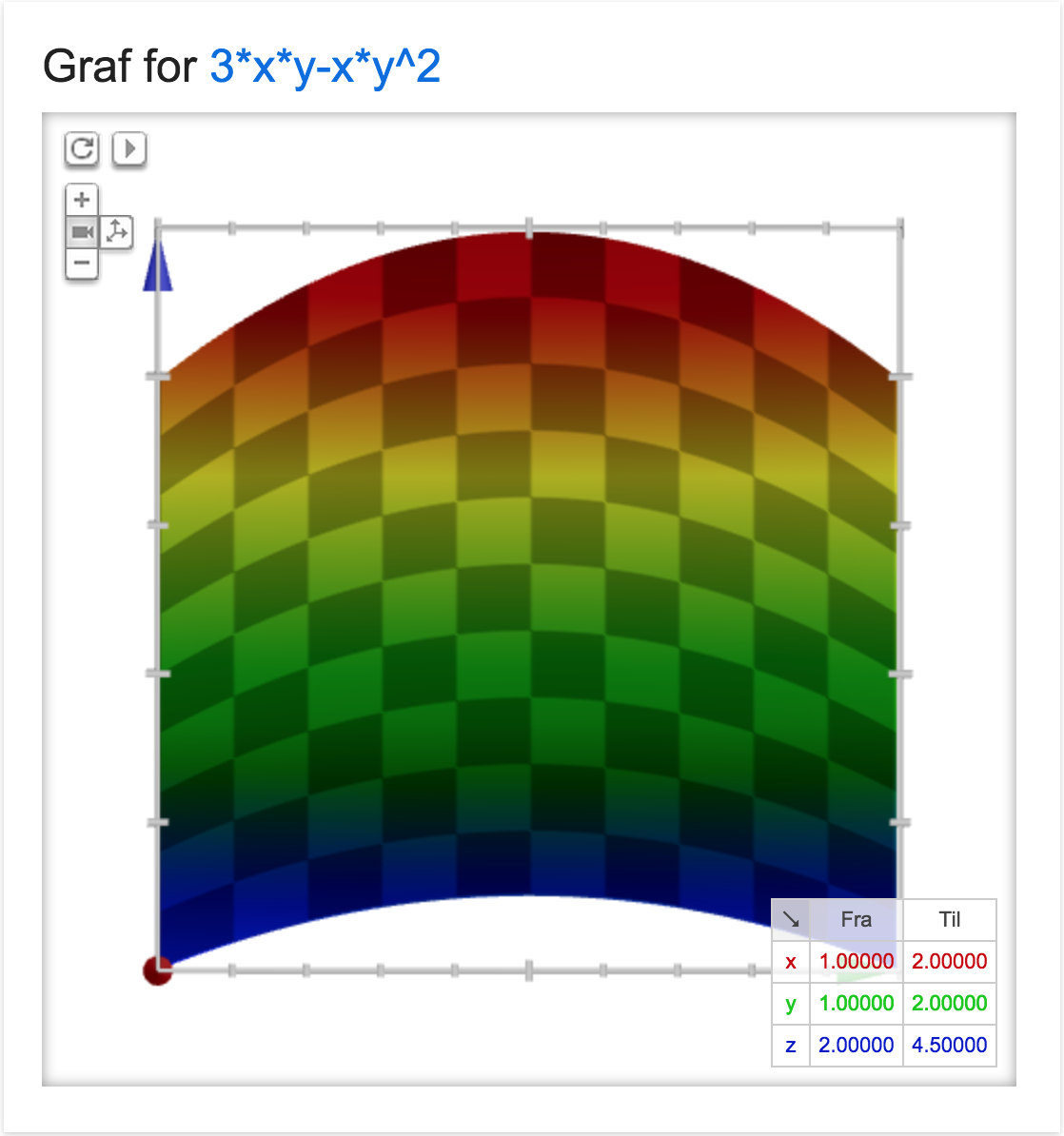
Denne graf er lavet i Google ved at søge på funktionsudtrykket (i blåt) og synes at vise, at funktionens værdier ligger mellem 2 og 4,5. Det er tænkt som en kontrol.

Vedhæftet fil:Screen Shot 2015-06-24 at 4.02.38 PM.png

Svar #2
24. juni 2015 af xLaila (Slettet)

Okay, betyder det så at maksimums- og minimumsværdien ligger mellem 2-4,5?

Brugbart svar (0)

Svar #3
24. juni 2015 af Soeffi

#2 Okay, betyder det så at maksimums- og minimumsværdien ligger mellem 2-4,5?

Ja, omtrent.

Brugbart svar (1)

Svar #4
24. juni 2015 af Soeffi

Prøv en rand-undersøgelse af f(x,y) = 3xy-xy²:

1 ≤ x ≤ 2, y = 1: f(x,1) = 2x => fmin = 2, fmax = 4

1 ≤ x ≤ 2, y = 2: f(x,2) = 2x => fmin = 2, fmax = 4

x = 1, 1 ≤ y ≤ 2: f(1,y) = 3y - y² => fmin = 2, fmax = 2,25

x = 2, 1 ≤ y ≤ 2: f(2,y) = 6y - 2y² => fmin = 4, fmax = 4,5

Brugbart svar (1)

Svar #5
24. juni 2015 af Toonwire

Ligger de kritiske punkter uden for mængden, kan du se bort fra dem - Idet du kun er interesseret i at finde min/maks på mængden.

Lav randundersøgelse samt find stationære punkter.
Hold en af parametrene fast og variér den anden, løs i intervallet
Gør dette for begge parametres intervalværdier

Herunder er alle de stationære-/randpunkter for funktionen på mængden, og disses værdier:

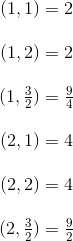
$\begin{matrix} (1, 1) = 2\\\\ (1, 2) = 2\\\\(1, \frac{3}{2}) = \frac{9}{4}\\\\(2, 1) = 4\\\\(2, 2) = 4\\\\(2, \frac{3}{2}) = \frac{9}{2}\end{matrix}$

Dvs. der findes minumum i punkterne 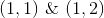hvor disse antager værdien 2.
og der findes maksimum i punktet 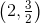med værdien

Svar #6
24. juni 2015 af xLaila (Slettet)

#5
Okay. I min randundersøgelse fik jeg kun de 4 nederste punkter, som du også har. Hvordan bestemte du punkterne (1,1) = 2 og (1,2) = 2?

Brugbart svar (0)

Svar #7
24. juni 2015 af Toonwire

Fasthold 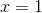og lad

Husk at undersøge randen, dvs. ydrepunkterne for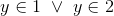

Altså netop punkterne (1,1) og (1,2)

Svar #8
24. juni 2015 af xLaila (Slettet)

Okay, tak for hjælpen. Men behøver man at specificere punkterne, fx Påpege hvilke af dem, som er globale og lokale maksimums- og minimumsværdier?

Brugbart svar (0)

Svar #9
24. juni 2015 af Toonwire

Det skader vel aldrig at vise mere indsigt? :)

Brugbart svar (0)

Svar #10
24. juni 2015 af Soeffi

Et billede der på en gang viser randen for x = 1 (nederst) og x = 2 (øverst). Begge er grafen for et andengradspolynomium. Skærmens plan er parallelt med y-z planen.

Vedhæftet fil:Screen Shot 2015-06-24 at 6.25.39 PM.png

Skriv et svar til: Matematik - Maksimums- og minimumsværdi (funktioner af 2 variable)

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.