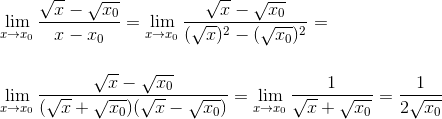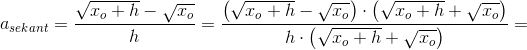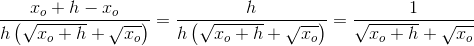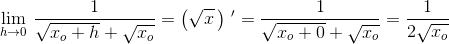Matematik

Bevis for differentiation af kvadratrod x

22. maj 2016 af 123434 - Niveau: B-niveau

Bevis for (√x)=1/(2*√x)

Trin 1

Finder y-tilvæksen

Δy=(fx₀+h)-f(x₀)

f(x₀+h)=√(x₀+h)

f(x₀)=√x₀

Δy=√(x₀+h)-√x₀

Trin 2

Vi har fundet y-tilvæksten i trin 1. Hældningen af sektanten kan findes ved a_s=Δy/h. hvor h er x-tilvæksten

a_s=(√(x₀+h)-√x₀)/h

Trin 3

Vi har fundet differenskvotienten(hældningen af sekanten) i trin 2.

Ved at gøre h uendelig lille, så vil differenskvotienten glide over differentialkvotienten(hældningen af tangenten)

a_t=lim(a_s)

h→0

a_t=lim(√(x₀+h)-√x₀)/h)=√x₀-√x₀

h→0

Jeg kan ikke rigtig få det til at give 1/(2√x)

Brugbart svar (0)

Svar #1
22. maj 2016 af Soeffi

#0

$\\\lim_{x\rightarrow x_0}\frac{\sqrt{x}-\sqrt{x_0}}{x-x_0}=\lim_{x\rightarrow x_0}\frac{\sqrt{x}-\sqrt{x_0}}{(\sqrt{x})^2-(\sqrt{x_0})^2}=\\\;\\\;\\ \lim_{x\rightarrow x_0}\frac{\sqrt{x}-\sqrt{x_0}}{(\sqrt{x}+\sqrt{x_0})(\sqrt{x}-\sqrt{x_0})}=\lim_{x\rightarrow x_0}\frac{1}{\sqrt{x}+\sqrt{x_0}}= \frac{1}{2\sqrt{x_0}}$

Brugbart svar (0)

Svar #2
22. maj 2016 af mathon

eller

$a_{sekant}=\frac{\sqrt{x_o+h}-\sqrt{x_o}}{h}=\frac{\left (\sqrt{x_o+h}-\sqrt{x_o} \right )\cdot\left ( \sqrt{x_o+h}+\sqrt{x_o} \right )}{h\cdot \left ( \sqrt{x_o+h}+\sqrt{x_o} \right )}=$

$\frac{x_o+h-x_o}{h\left ( \sqrt{x_o+h}+\sqrt{x_o} \right )}=\frac{h}{h\left ( \sqrt{x_o+h}+\sqrt{x_o} \right )}=\frac{1}{\sqrt{x_o+h}+\sqrt{x_o}}$

$\underset{h \to 0}{\lim} \, \, \frac{1}{\sqrt{x_o+h}+\sqrt{x_o}}=\left ( \sqrt{x} \, \right ){\, }'=\frac{1}{\sqrt{x_o+0}+\sqrt{x_o}}=\frac{1}{2\sqrt{x_o}}$

Svar #3
26. maj 2016 af 123434

Fandt faktisk ud af, at man kunne udføre beviset langt nemmere uden tretrinsreglen og i stedet benytte potensreglerne og reglen (xⁿ)'=n*x^n-1

Sætning

Når g(x)=√x, så er g'(x)=1/(2√x)

Omskriver g(x)=√x til g(x)=x^1/2. Der gælder nemlig potensregnereglen √x=x^1/2

g(x)=x^1/2

Benytter differentationsreglen (xⁿ)'=n*x^n-1

(x^1/2)'=1/2*x^1/2-1=1/2x^-1/2

g'(x)=1/2*x^-1/2

Benytter at x^-1/2=1/√x

g'(x)=1/2*1/√x=1/(2√x)

Brugbart svar (0)

Svar #4
26. maj 2016 af Stats

Problemet ligger vel i, at man antager at (xⁿ)'=n*x^n-1 gælder for alle n∈R\{0}.

- - -

Mvh Dennis Svensson

Skriv et svar til: Bevis for differentiation af kvadratrod x

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.