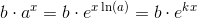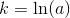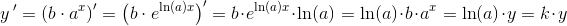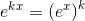Matematik
Mundtlig Mat A
Hej.
Er der nogle søde mennesker, som gerne vil forklare mig præcis hvad der bliver spurtg efter her. Det er sidste års mundtlig prøve:
Vækst: Forklar om eksponentialfunktioner, 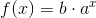 Bevis en sætning om differentialligninger, hvor den naturlige eksponentialfunktion indgår som løsning.
Bevis en sætning om differentialligninger, hvor den naturlige eksponentialfunktion indgår som løsning.
Sådan som jeg forstår det, skal jeg starte med at forklare eksponentiel funktion (det basiske altså hvad b og a er, funktionen er voksende hvis a>1 osv.) Men forstår bare ikke det sidste hvor "Bevis en sætning om differentialligninger, hvor den naturlige eksponentialfunktion indgår som løsning."
Altså skal jeg ikke bevise bestemmelse af en eksponentiel funktion, der går gennem 2 punkter?
Eller skal jeg bevise mere?
Svar #2
09. juni 2016 af Britagnita (Slettet)
Okay. Kan simpelthen ikke finde det i min Mat bog, men kan du rekommendere en hjemmeside måske, hvor der er noget relevant indhold?
Svar #4
09. juni 2016 af Sfeldt (Slettet)
følgende differentialligninger
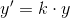 og
og
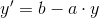
har henholdvis
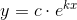 og
og 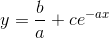 som løsning.
som løsning.
Det skal du bare bevise. Så her går spørgsmålet over til et spørgsmål om differentialligninger.
Svar #5
09. juni 2016 af Sfeldt (Slettet)
Den letteste måde at bevise det på er at sætte løsningen ind i differentialligningen og se, om ligningen bliver sandt.
Svar #6
09. juni 2016 af mathon
efter separation af de variable x og y
haves
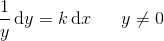 hvorefter der integreres på bege sider:
hvorefter der integreres på bege sider:
Svar #8
09. juni 2016 af mathon
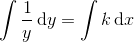
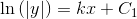
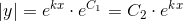
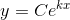
som er den fuldstændige løsning til differentialligningen
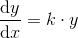
efterprøvning
giver
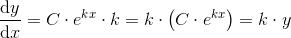
Svar #9
09. juni 2016 af Britagnita (Slettet)
Men hvor indgår den naturlige eksponential funktion som løsning?
Er vi ikke enige om at, den naturalige er f(x)= e^x ?
Svar #11
09. juni 2016 af Britagnita (Slettet)
Hmm.. så vi ved at 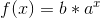 er en løsning til
er en løsning til 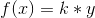 ?
?
Men hvordan finder heg så at den naturlige eksponentielle funktion indgår som en løsning?
Argh, tror jeg forstår! Nu, da der er bevist at [f(x)=b*a^x] er en løsning til [f(x)=k*y], så skal jeg bevise at [f(x)=k*y] har den eksponentielle funktion som en løsning?
Svar #13
09. juni 2016 af Britagnita (Slettet)
Det du siger er, at 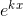 er en løsning til
er en løsning til 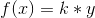 ?
?
Altså ligesom bevist i denne video?
Skriv et svar til: Mundtlig Mat A
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.





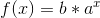 og
og 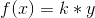 ?
?