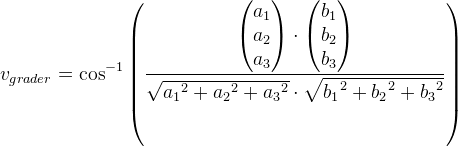Matematik
vektorer
30. juli 2016 af
Mallingg (Slettet)
-
Niveau: A-niveau
Jeg sidder med et problem som jeg er i tvivl om. Hvis vi siger at vi skal finde vinklen mellem 2 vektorer i rummet. Vi får opgivet en parameterfremstilling hvor der er et punkt og vores retningsvektor.
Hvis jeg nu skal bruge cos(v)=vektor a prikket med vektor b og så divideret med længden, hvordan finder jeg så vektor a og b?
Jeg ved man finder retningsvektoren ved at trække 2 punkter fra hinanden og det. Jeg ved at jeg skal gøre noget med retningsvektoren og punktet, men hvordan? Derudover er der jo også de 2 ubekendte s og t som er hvor langt vi går ud til punktet.
Så mit spørgsmål er hvordan man finde vektor a og b ud fra retningsvektor og punkt hvor der også er 2 parameterfremstillinger for 2 linjer
Mallingg
Hvis jeg nu skal bruge cos(v)=vektor a prikket med vektor b og så divideret med længden, hvordan finder jeg så vektor a og b?
Jeg ved man finder retningsvektoren ved at trække 2 punkter fra hinanden og det. Jeg ved at jeg skal gøre noget med retningsvektoren og punktet, men hvordan? Derudover er der jo også de 2 ubekendte s og t som er hvor langt vi går ud til punktet.
Så mit spørgsmål er hvordan man finde vektor a og b ud fra retningsvektor og punkt hvor der også er 2 parameterfremstillinger for 2 linjer
Mallingg
Svar #3
30. juli 2016 af Mallingg (Slettet)
Så jeg kan altså godt sige r1=vektor a og r2=vektor b?
Nårhh... Det er jo derfor at vi bruger vektorer da man ikke skal finde længden til punktet for at kende vinklen.
Nårhh... Det er jo derfor at vi bruger vektorer da man ikke skal finde længden til punktet for at kende vinklen.
Svar #4
30. juli 2016 af Mallingg (Slettet)
Jeg kendte godt formlen og fremgangsmåden men var i tvivl om jeg kunne bruge r som vektor
Skriv et svar til: vektorer
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.