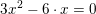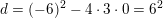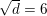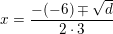Matematik
Andengradsligning, find ligningen for de to tangenter med hældningen 1
22. september 2017 af
PernGM
-
Niveau: A-niveau
F(x) = x^3 -3x^2 + x
Bestem ligningerne for de to tangenter der har hældningskoefficienten 1.
Har svært ved at finde ud af,hvordan jeg skal gribe denne opgave an. Nogne der kan hjælpe?
Svar #2
22. september 2017 af PernGM
Undskyld - væsentligt detalje: jeg skal løse opgaven uden hjælpemidler.
Skriv et svar til: Andengradsligning, find ligningen for de to tangenter med hældningen 1
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.




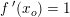 hvor
hvor 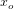 søges.
søges.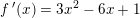
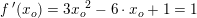
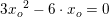
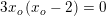 …
…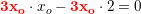 sæt fælles faktor uden for parentes.
sæt fælles faktor uden for parentes.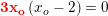 brug nu nulreglen.
brug nu nulreglen.