Matematik

På figuren ses skitse af graferne for to funktioner f og g

16. november 2017 af Rensm (Slettet) - Niveau: A-niveau

Graferne for f og g afgrænser en punktmængde M, der har et areal.

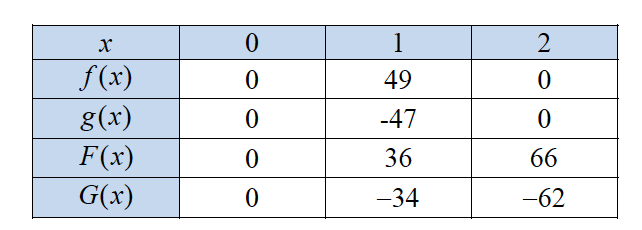
Tabellen viser nogle funktionsværdier for funktionerne f, g, F og G hvor F og G betegner hhv. en stamfunktion til f og en stamfunktion til g.

Jeg har vedhæftet tabellen!

Jeg skal bestemme arealet af M, men er desværre ikke helt med på, hvordan jeg skal gribe opgaven an.

Tak!

Vedhæftet fil: Skærmbillede 2017-11-16 kl. 20.23.02.png

Brugbart svar (0)

Svar #1
16. november 2017 af SådanDa

Læs evt. her:

http://www.webmatematik.dk/lektioner/matematik-a/integralregning/areal-mellem-to-funktioner

Brugbart svar (0)

Svar #2
16. november 2017 af Mathias7878

$\small M = \int_{0}^{2}f(x)-g(x)dx = (F(2)-G(2))-(F(0)-G(0))$

- - -

Brugbart svar (0)

Svar #3
16. november 2017 af peter lind

Brugbart svar (0)

Svar #4
16. november 2017 af peter lind

Areal = ∫₀²f(x)dx = F(2)-F(0)

For g(x) finder du arealet på lignende måde

Svar #5
16. november 2017 af Rensm (Slettet)

Nåå, skal jeg trække 66 fra 36?

Svar #6
16. november 2017 af Rensm (Slettet)

Hvad indsætter man på f(x) og g(x) i formlen?

Brugbart svar (2)

Svar #7
16. november 2017 af Mathias7878

I forlængelse af #2:

$\small M = \int_{0}^{2}f(x)-g(x) = (F(2)-G(2))-(F(0)-G(0)) = 66-(-62)-0 = 128$

- - -

Brugbart svar (0)

Svar #8
26. februar 2021 af Emilie76

#4
Areal = ∫₀²f(x)dx = F(2)-F(0)

For g(x) finder du arealet på lignende måde

Hvilket tal sætter du ind og hvordan kommer regnestykket til at se ud?

Brugbart svar (0)

Svar #9
26. februar 2021 af ringstedLC

I #7 er indsat de værdier, der kan aflæses i tabellen.

Brugbart svar (0)

Svar #10
27. februar 2021 af Emilie76

#9
I #7 er indsat de værdier, der kan aflæses i tabellen.

så F(x)= 66-0 og G(x)= -62-0 eller ?

Brugbart svar (0)

Svar #11
28. februar 2021 af ringstedLC

#10: Nej. Stamfunktionerne kan ikke være konstanter, da:

$\begin{array} {lll} F(x)=k_1\Rightarrow F'(x)=f(x)=0\neq \;\;\,49=f(1) \\ G(x)=k_2\Rightarrow G'(x)=g(x)=0\neq -47=g(1) \end{align*}$

Når funktionsværdierne ved integrationsgrænserne oplyses:

$\begin{align*} &\left.\begin{matrix} f(0)=f(2)=0\wedge f(1)=49 \\ g(0)=g(2)=0\wedge g(1)=-47\end{matrix}\right\}\Rightarrow f(x)\geq 0\geq g(x) \end{align*}$

Når integralerne ved integrationsgrænserne oplyses:

$\begin{align*} M &= \int_{0}^{2}\!f(x)\,\mathrm{d}x -\int_{0}^{2}\!g(x)\,\mathrm{d}x\\ &= F(2)-F(0)-\Bigl(G(2)-G(0)\Bigr) \\ M&= 66-0-(-62-0)=128 \end{align*}$

Skriv et svar til: På figuren ses skitse af graferne for to funktioner f og g

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.