Matematik

Vektorregning

13. marts 2018 af Mathian - Niveau: A-niveau

Igang med opgave 2, som jeg finder en smule udfordrende, da der er gået lidt tid imellem kapitlerne.

Men dette er mit bud, håber der er en venlig sjæl derude som vil kigge med og rette opgaven:

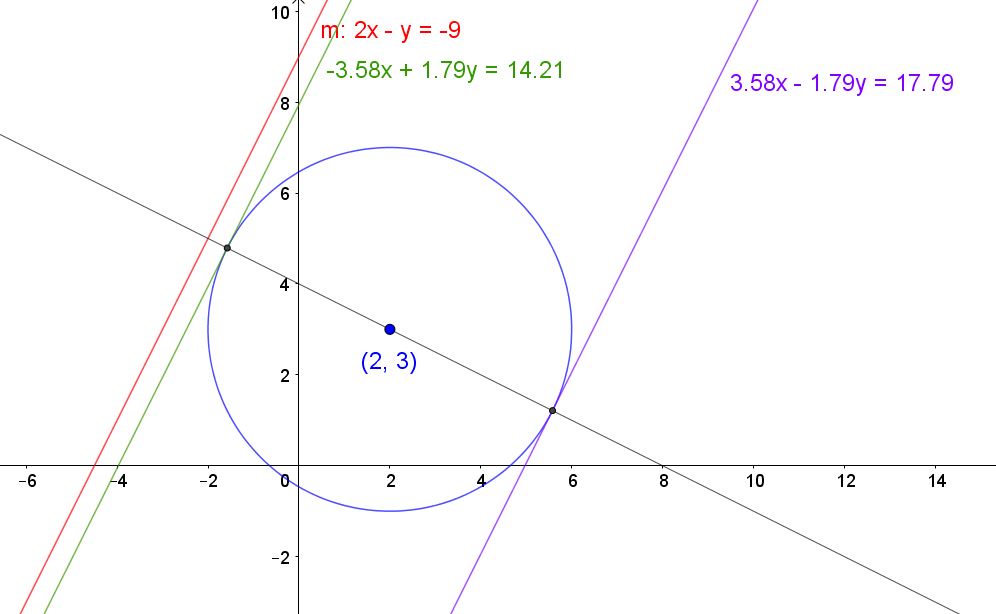
2) Vi bestemmer ligningen for den rette linje, der er ortogonal på m, og som går gennem cirklens centrum, vi tager udgangspunktet i sætningen, der siger at når to retningsvektorer er ortogonale, er produktet af deres hældningskoefficienter (-1). Vores ligning m, har hældningen 4, linjen skal have hældningen -1/4 da:

$4*(-1/4)=-1$

Vi former vores ligning med udgangspunkt i punktet for cirklens centrum, og isolerer herefter b:

$3=-1/4 *2+b$

$b=1/2+3 = 3,5$

$y=-1/2x+3.5$

Vi indsætter i cirklens ligning for at finde skæringspunkterne:

$(x-2)+(-1/2+3.5-3)^2=4^2$

$x=18$

Vedhæftet fil: Skærmbillede 2018-03-13 kl. 05.24.22.png

Brugbart svar (0)

Svar #1
13. marts 2018 af PeterValberg

Du har glemt, at (x - 2) også skal kvadreres:

$(x-2)^{\color{Red} 2}+(-\tfrac12+\, 3,5-3)^2=4^2$

desuden skal du jo forvente to skæringspunkter

- - -

mvh.

Peter Valberg
(YouTube)

Svar #2
13. marts 2018 af Mathian

Ja, det sandt. Det var faktisk også motivet bag indlægget, men takker for din hjælp, den er stor :)

Svar #3
13. marts 2018 af Mathian

Hvis jeg gerne vil finde deres tilhørende y-værdier, er det cirklens ligning, jeg skal bruge eller linjens?

Brugbart svar (0)

Svar #4
13. marts 2018 af PeterValberg

Det er nok lettest, hvis du benytter ligningen for linjen
gennem punkterne (og cirklens centrum)

- - -

mvh.

Peter Valberg
(YouTube)

Brugbart svar (0)

Svar #5
13. marts 2018 af PeterValberg

En ligning for tangenterne til cirklen gennem punkterne, - som du skal bestemme i 3)
kan bestemmes vha.:

$a(x-x_0)+b(y-y_0)=0$

hvor (x₀, y₀) er koordinaterne til det aktuelle røringspunkt
a og b er hhv. x- og y-koordinaten til en normalvektor for tangenten,
og da tangenterne skal være parallelle med m, kan du benytte dennes
normalvektor n_m = (4,-2) ... hvilket aflæses af ligningen for m

- - -

mvh.

Peter Valberg
(YouTube)

Brugbart svar (0)

Svar #6
13. marts 2018 af PeterValberg

Tegningen kan du lave i fx GeoGebra

- - -

mvh.

Peter Valberg
(YouTube)

Vedhæftet fil:Udklip.JPG

Brugbart svar (0)

Svar #7
13. marts 2018 af mathon

som du fik svar på i
https://www.studieportalen.dk/forums/thread.aspx?id=1817399

$\small \textup{Til beregning af r\o ringspunkter:}$

$\small \overrightarrow{OR}=\overrightarrow{OC}\mp r\cdot \frac{\overrightarrow{n}}{\left | \overrightarrow{n} \right |}$

$\small \overrightarrow{OR}=\overrightarrow{OC}\mp \frac{r}{\left | \overrightarrow{n} \right |}\cdot \overrightarrow{n}$

$\small \begin{pmatrix} x\\y \end{pmatrix}=\begin{pmatrix} 2\\3 \end{pmatrix}\mp \frac{4}{2\sqrt{5}}\cdot \begin{pmatrix} 4\\-2 \end{pmatrix}$

$\small \textup{hvoraf med \textbf{minustegnet}:}$
$\small \begin{pmatrix} x\\y \end{pmatrix}=\begin{pmatrix} 2\\3 \end{pmatrix}- \frac{4}{2\sqrt{5}}\cdot \begin{pmatrix} 4\\-2 \end{pmatrix}=\begin{pmatrix} 2-8\sqrt{5}\\ 3+4\sqrt{5} \end{pmatrix}\approx \begin{pmatrix} -15{.}89\\ 11{.}94 \end{pmatrix}$

$\small \small \textup{hvoraf med \textbf{plustegnet}:}$
$\small \begin{pmatrix} x\\y \end{pmatrix}=\begin{pmatrix} 2\\3 \end{pmatrix}+ \frac{4}{2\sqrt{5}}\cdot \begin{pmatrix} 4\\-2 \end{pmatrix}=\begin{pmatrix} 2+8\sqrt{5}\\ 3-4\sqrt{5} \end{pmatrix}\approx \begin{pmatrix} 19.89\\ -5.94 \end{pmatrix}$

Brugbart svar (0)

Svar #8
13. marts 2018 af mathon

og tangenterne:
$\small \small 2x-y+\left ( 20\sqrt{5}- 1\right )=0$

$\small 2x-y-\left ( 20\sqrt{5}+ 1\right )=0$

Brugbart svar (0)

Svar #9
13. marts 2018 af mathon

$\small \textup{Jeg har nu f\aa et rystet morgens\o vnen ud af \o jnene}$
$\small \small \small \textup{og derfor opdaget en forglemmelse af n\ae vner: }5\; \; \textbf{:-)}$

$\small \textup{hvoraf med \textbf{minustegnet}:}$
$\small \begin{pmatrix} x\\y \end{pmatrix}=\begin{pmatrix} 2\\3 \end{pmatrix}- \frac{4}{2\sqrt{5}}\cdot \begin{pmatrix} 4\\-2 \end{pmatrix}=\begin{pmatrix} 2-\frac{8\sqrt{5}}{5}\\ 3+\frac{4\sqrt{5}}{5} \end{pmatrix}\approx \begin{pmatrix} -1{.}58\\ 4{.}79 \end{pmatrix}$

$\small \small \textup{hvoraf med \textbf{plustegnet}:}$
$\small \begin{pmatrix} x\\y \end{pmatrix}=\begin{pmatrix} 2\\3 \end{pmatrix}+ \frac{4}{2\sqrt{5}}\cdot \begin{pmatrix} 4\\-2 \end{pmatrix}=\begin{pmatrix} 2+\frac{8\sqrt{5}}{5}\\ 3-\frac{4\sqrt{5}}{5} \end{pmatrix}\approx \begin{pmatrix} 5.58\\ 1.21 \end{pmatrix}$

Brugbart svar (0)

Svar #10
13. marts 2018 af mathon

og tangenterne:
$\small \small \small 2x-y+\left ( 4\sqrt{5}- 1\right )=0$ eller $\small y=2x+\left ( 4\sqrt{5}-1 \right )$

$\small 2x-y-\left ( 4\sqrt{5}+ 1\right )=0$ eller $\small y=2x-\left ( 4\sqrt{5}+1 \right )$

Svar #11
13. marts 2018 af Mathian

Mange tak for hjælpen.

Jeg fik x-værdierne til x= -2 og x= 6 ud fra ovenfornævnte metode, det ville ikke være rigtigt?

Ps: Tak for hjælpen Mathon, villle bare prøve grundbogens metode ad.

Brugbart svar (0)

Svar #12
13. marts 2018 af mathon

$\small \textup{ALTERNATIVT}$

$\small \textup{Til beregning af r\o ringspunkter:}$

$\small \textup{en normalvektor til tangenterne er: }\overrightarrow{n}=\begin{pmatrix} 2\\-1 \end{pmatrix}}$
$\small \textup{og dermed er en retningsvektor for tangenterne: }\overrightarrow{r}=\widehat{\overrightarrow{n}}=\begin{pmatrix} 1\\2 \end{pmatrix}$
$\small \textup{dvs h\ae ldningskoefficienten for tangenterne er } \frac{\mathrm{d} y}{\mathrm{d} x}=\textbf{2}.$

$\small \textup{Tangenth\ae ldning 2 er kun mulig i \small \textup{\o vre venstre kvartcirkel og i nedre h\o jre kvartcirkel.}}$

$\small \textup{For cirkelpunkter i \o vre venstre kvartcirkel g\ae lder:}$

$\small x=2-\frac{4}{\sqrt{1+\left (\textbf{2} \right )^{-2}}}=2-\frac{8\sqrt{5}}{5}$

$\small y=3+\sqrt{16-\left (2-\frac{8\sqrt{5}}{5}-2 \right )^2}=3+\frac{4\sqrt{5}}{5}$

$\small \textup{For cirkelpunkter i \o vre venstre kvartcirkel g\ae lder:}$    $\small -2<x<2\textup{ og }3<y<7$

      $\small x=2-\frac{4}{\sqrt{1+\left (\textbf{2} \right )^{-2}}}=2-\frac{8\sqrt{5}}{5}$

$\small y=3+\sqrt{16-\left (2-\frac{8\sqrt{5}}{5}-2 \right )^2}=3+\frac{4\sqrt{5}}{5}$

$\small \textup{For cirkelpunkter i nedre h\o jre kvartcirkel g\ae lder:}$    $\small 2<x<6\textup{ og }-1<y<3$

      $\small x=2+\frac{4}{\sqrt{1+\left (\textbf{2} \right )^{-2}}}=2+\frac{8\sqrt{5}}{5}$

$\small y=3-\sqrt{16-\left (2-\frac{8\sqrt{5}}{5}-2 \right )^2}=3-\frac{4\sqrt{5}}{5}$

Brugbart svar (0)

Svar #13
13. marts 2018 af mathon

$\small \textup{Man kan for cirklen:}$

$\small \left ( x-c_1 \right )^2+\left ( y-c_2 \right )^2=r^2$

$\small \textup{udlede:}$

$\small x=c_1\pm \frac{r}{\sqrt{1+\left (\frac{\mathrm{d} y}{\mathrm{d} x} \right )^{-2}} }$

Svar #14
14. marts 2018 af Mathian

Mange tak :)

Skriv et svar til: Vektorregning

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.