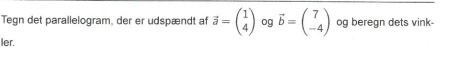Matematik

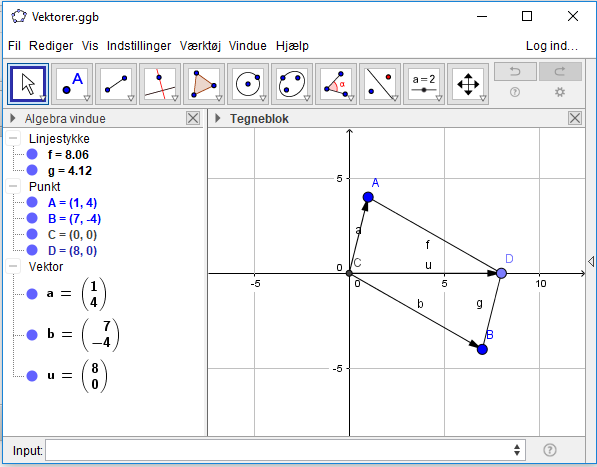
Er den tegnet korrekt

10. august 2018 af hannah9 - Niveau: B-niveau

er usikker på den

Vedhæftet fil: vregning.PNG

Svar #1
10. august 2018 af hannah9

opgave her

Vedhæftet fil:ny.PNG

Brugbart svar (0)

Svar #2
10. august 2018 af PeterValberg

Vektorerne er korrekt indtegnet, så mangler du bare
at færdiggøre parallelogrammet, som de udspænder
samt at bestemme vinklerne.

- - -

mvh.

Peter Valberg
(YouTube)

Brugbart svar (0)

Svar #3
10. august 2018 af mathon

Brugbart svar (0)

Svar #4
10. august 2018 af mathon

$\small \textup{Vektorernes skalarprodukt:}$
$\small \overrightarrow{a}\cdot \overrightarrow{b}=\begin{pmatrix} 1\\4 \end{pmatrix}\cdot \begin{pmatrix} 7\\-4 \end{pmatrix}=1\cdot 7+4\cdot (-4)=-9$
$\small \textup{med vektorl\ae ngderne:}$
$\small \left | \overrightarrow{a} \right |=\sqrt{1^2+4^2}=\sqrt{17}$ $\small \left | \overrightarrow{b} \right |=\sqrt{7^2+(-4)^2}=\sqrt{65}$

$\small \textup{...til brug for vinkelberegningen.}$

Svar #5
10. august 2018 af hannah9

hvad mener du med

så mangler du bare
at færdiggøre parallelogrammet, som de udspænder?

Svar #6
10. august 2018 af hannah9

hvordan gør man det?

Brugbart svar (0)

Svar #7
10. august 2018 af mathon

$\textup{I et parallellogram er de modst\aa ende sider parallelle og lige lange.}$

$\textup{dvs med vinkelspidser i (0,0), (1,4), {\color{Red} (8,0)} og (7,-4).}$

Svar #8
10. august 2018 af hannah9

så jeg skal sætte (0,0,) Og (8,0) ind ?

Brugbart svar (0)

Svar #9
10. august 2018 af mathon

Ja og indtegne siderne mellem disse punkter/vinkelspidser.

Svar #10
10. august 2018 af hannah9

ser det rigtigt ud nu?

Vedhæftet fil:her h.PNG

Brugbart svar (1)

Svar #11
10. august 2018 af Eksperimentalfysikeren

Koordinaterne til A, B og C skal være hele tal.

Hvor har du f og g fra?

Svar #12
10. august 2018 af hannah9

så du siger jeg skal fjerne f og g

Brugbart svar (1)

Svar #13
10. august 2018 af StoreNord

Nej.

Vedhæftet fil:Vektorer.PNG

Brugbart svar (0)

Svar #14
12. august 2018 af mathon

$\small \textup{vinkelberegning:}$

$\small \overrightarrow{a}=\begin{pmatrix} 1\\4 \end{pmatrix}\; \; \; \; \; \overrightarrow{a}=\begin{pmatrix} 7\\-4 \end{pmatrix}$
                                $\small \overrightarrow{a}\cdot \overrightarrow{b}=\begin{pmatrix} 1\\4 \end{pmatrix}\cdot \begin{pmatrix} 7\\-4 \end{pmatrix}=1\cdot 7+4\cdot (-4)=-9$
                                $\small \left |\overrightarrow{a} \right |=\sqrt{1^2+4^2}=\sqrt{17}$
                                $\small \left |\overrightarrow{b} \right |=\sqrt{7^2+(-4)^2}=\sqrt{65}$
                                $\small \cos(v)=\frac{\overrightarrow{a}\cdot \overrightarrow{b}}{\left |\overrightarrow{a} \right |\cdot \left |\overrightarrow{b} \right |}=\frac{-9}{\sqrt{17}\cdot \sqrt{85}}=-0.270746$

$\small v=\cos^{-1}(-0.270746)=105.7\degree$

$\small 180\degree-v=180\degree-105.7\degree=74.3\degree$

$\small \textup{I et parallellogram er de modst\aa ende vinkler lige store og vinkler op mod samme side er supplementvinkler.}$

Brugbart svar (0)

Svar #15
12. august 2018 af StoreNord

$\small \cos(v)=\frac{\overrightarrow{a}\cdot \overrightarrow{b}}{\left |\overrightarrow{a} \right |\cdot \left |\overrightarrow{b} \right |}=\frac{-9}{\sqrt{17}\cdot \sqrt{85}}=-0.270746$ $\sqrt{85}\: \; skal \; v\ae re\; \sqrt{65}$ , men facit er rigtigt.

Skriv et svar til: Er den tegnet korrekt

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.