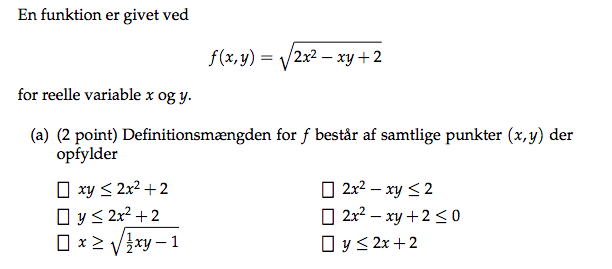Matematik

Hvordan kan man se dette

10. januar 2019 af Warrio - Niveau: Universitet/Videregående

Hej

Jeg har oploaded en opgave, som et billede. Jeg er ikke særlig god til se sådan nogle type opgave, og har aldrig kunne forstå det. Er der en metode, for at se hvad/hvordan det gælder?

På forhånd tak!

Vedhæftet fil: Screen Shot 2019-01-10 at 16.22.09.png

Brugbart svar (0)

Svar #1
10. januar 2019 af swpply (Slettet)

Brugbart svar (0)

Svar #2
10. januar 2019 af swpply (Slettet)

Da "indmaden" af en kvadratrod ikke er entydigt veldefineret for negative tal, har du at

$\text{Dm}(f) = \{(x,y)\in\mathbb{R}^2\mid 2x^2-xy+2\geq 0\}$

hvilket er ækvivalent med svarmulighed a.

Svar #3
10. januar 2019 af Warrio

Okay.

Så et sprørgsmål til samme opgave. Hvordan kan man bestemme en kritisk punkt udfra denne funktion.

Man skal vel bestemme $f_{x}$ og $f_{y}$ ikke?

Brugbart svar (0)

Svar #4
10. januar 2019 af swpply (Slettet)

#2
Da "indmaden" af en kvadratrod ikke er entydigt veldefineret for negative tal [...]

Det er selvfølgelig noget være vås, der skulle istedet havde stået: Da kvadratrod ikke er entydigt veldefineret for negative tal, har du at [...]

Svar #5
10. januar 2019 af Warrio

Når der er tale om en kritisk punkt, hvordan finder man dette?

Er det ikke ved at bestemme $f_{x}$ og $f_{y}$ og sætter dem = 0 ?

Brugbart svar (0)

Svar #6
10. januar 2019 af oppenede

#5 Fjern kvadratroden først, da den er strengt voksende og derfor ikke påvirker hvilke punkter der er kritiske.

Svar #7
10. januar 2019 af Warrio

Kan jeg gøre dette, ved bare at sige jeg opløfter det hele i anden

Svar #8
10. januar 2019 af Warrio

Kan det passe, at det er (0,0)?

Skriv et svar til: Hvordan kan man se dette

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.