Matematik

Størst mulige areal af trekant

06. maj 2019 af meitner - Niveau: B-niveau

Hej,

Jeg sidder med vedhæftede opgave og har lavet a. Jeg skal til b, men jeg ved ikke hvordan den skal gribes an. Jeg tænker, at det er optimering, men jeg ved ikke helt?

Vedhæftet fil: Skærmbillede 2019-05-06 kl. 16.02.33.png

Brugbart svar (2)

Svar #1
06. maj 2019 af AMelev

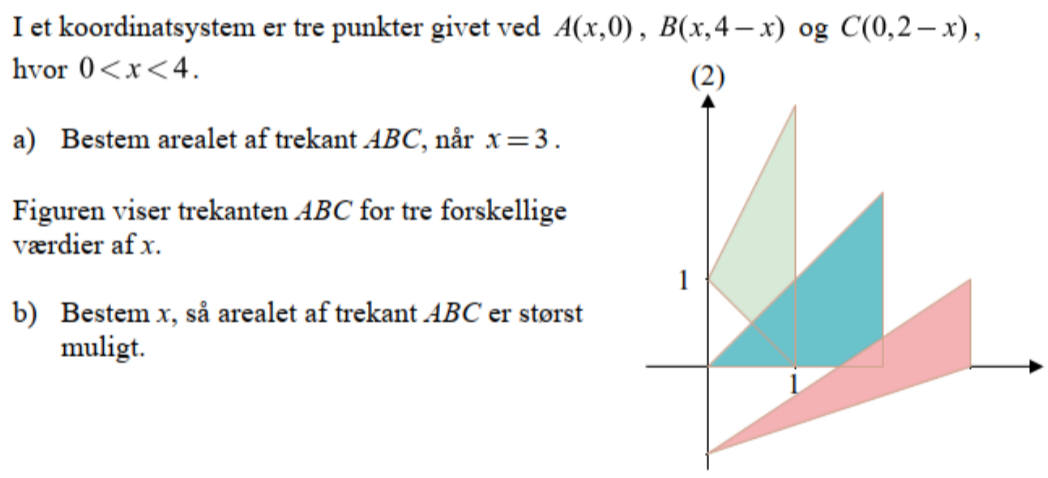
Bestem koordinatsættet til to af de udspændende vektorer, fx $\overrightarrow{CA}$ og $\overrightarrow{CB}$ .
Bestem arealet af trekanten = ½·parallelogram-areal (FS s. 12 (61))
Arealet er en funktion f(x). Bestem max for f på sædvanlig vis.

Brugbart svar (2)

Svar #2
06. maj 2019 af mathon

$\begin{array}{lllll} b)&&T(x)=\frac{1}{2}\cdot x\cdot (4-x)=2x-\frac{1}{2}x^2&&0<x<4\\\\ &&T{\, }'(x)=2-x\\\\ &T_{max}\textup{ kr\ae ver bl.a.}&T{\, }'(x)=2-x=0 \end{array}$

Svar #3
06. maj 2019 af meitner

Men jeg forstår ikke, fordi gælder T(x) = 0.5 * x * y ikke kun ved retvinklede trekanter?

Brugbart svar (0)

Svar #4
06. maj 2019 af mathon

$\small \begin{array}{lllll} T=\frac{1}{2}\cdot \textup{h\o jde}\cdot \textup{grundlinje}=\frac{1}{2}\cdot x\cdot (4-x) \end{array}$

Brugbart svar (0)

Svar #5
07. maj 2019 af AMelev

Bug determinantformlen til bestemmelse af areal af parallelogrammet udspændt af de to vektorer og tag halvdelen af det. Jf #1.

Brugbart svar (0)

Svar #6
08. maj 2019 af mathon

Determinantformlen giver naturligvis samme resultat:

$\small \begin{array}{lllll} \overrightarrow{CA}=\begin{pmatrix} x-0\\0-(2-x) \end{pmatrix}=\begin{pmatrix} x\\ x-2 \end{pmatrix}&&&\overrightarrow{CB}=\begin{pmatrix} x-0\\4-x-(2-x) \end{pmatrix}=\begin{pmatrix} x\\ 2 \end{pmatrix} \end{array}$

$\small T(x)=\frac{1}{2}\cdot \begin{vmatrix} x &x \\ x-2&2 \end{vmatrix}=\tfrac{1}{2}\cdot \left (2x-(x-2)x \right )=\tfrac{1}{2}\cdot \left (4x-x^2 \right )=2x-\tfrac{1}{2}x^2$

Skriv et svar til: Størst mulige areal af trekant

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.