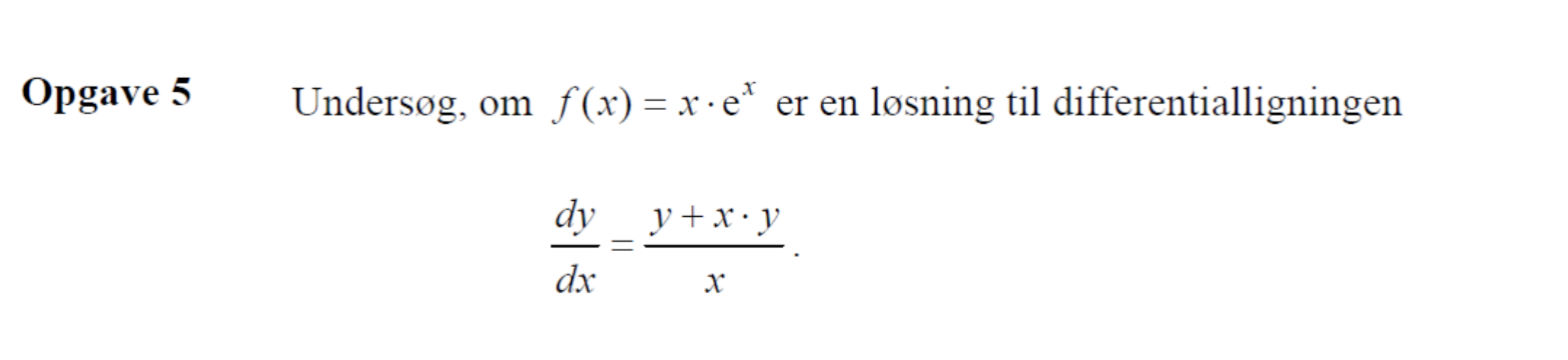Matematik

Bestem ligningen for tangenten til grafen for f i p(3,1)

19. maj 2019 af masteren123 - Niveau: A-niveau

Jeg får svaret til at give:

$y=9x-26$

Er det korrekt

Vedhæftet fil: Skærmbillede 2019-05-19 kl. 11.23.03.png

Brugbart svar (0)

Svar #1
19. maj 2019 af mathon

Svar #2
19. maj 2019 af masteren123

Ja det er spørgsmålet

Brugbart svar (1)

Svar #3
19. maj 2019 af mathon

$\small \begin{array}{lllll} \textup{tangentligning i (3,1):}&y=(3\cdot 1+2\cdot 3)(x-3)+1\\\\ &y=9(x-3)+1\\\\ &y=9x-26 \end{array}$

Svar #4
19. maj 2019 af masteren123

tak. Det var ogs¨det havde kom frem til

Svar #5
19. maj 2019 af masteren123

@mathon kan du yderkigere også hjælpe med dette spørgsmål.

Jeg får svaret til at give, at det IKKE er løsningen

Vedhæftet fil:Skærmbillede 2019-05-19 kl. 11.23.03.png

Brugbart svar (0)

Svar #6
19. maj 2019 af Mathias7878

Du har vedhæftet det samme billede som i #0.

- - -

Svar #7
19. maj 2019 af masteren123

Min fejl her var spørgsmålet

Vedhæftet fil:Skærmbillede 2019-05-19 kl. 11.32.54.png

Brugbart svar (0)

Svar #8
19. maj 2019 af mathon

Brugbart svar (1)

Svar #9
19. maj 2019 af mathon

Hvis
$\small y=x\cdot e^x\Leftrightarrowxy=x\cdot y=x^2\cdot e^x$
og
$\small \frac{y}{x}=e^x$

er
$\small \frac{\mathrm{d} y}{\mathrm{d} x}=1\cdot e^x+x\cdot e^x=\frac{y}{x}+y=\frac{y+y\cdot x}{x}=\frac{y+x\cdot y}{x}$

Altså er
$\small f(x)=x\cdot e^x$ en løsning til differentialligningen $\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{y+x\cdot y}{x}\qquad x\neq0$

Svar #10
19. maj 2019 af masteren123

Dvs det er ikke løsning, korrekt?

Brugbart svar (0)

Svar #11
19. maj 2019 af Mathias7878

#10 som vist i #9 er f(x) = x*e^x en løsning til differentialligningen.

- - -

Brugbart svar (0)

Svar #12
19. maj 2019 af mathon

Hvis
      $\small \small y=x\cdot e^x \Leftrightarrow xy=x\cdot y=x^2\cdot e^x$
og
      $\small \frac{y}{x}=e^x$

er
$\small \frac{\mathrm{d} y}{\mathrm{d} x}=1\cdot e^x+x\cdot e^x=\frac{y}{x}+y=\frac{y+y\cdot x}{x}=\frac{y+x\cdot y}{x}$

Altså er
$\small f(x)=x\cdot e^x$ en løsning til differentialligningen $\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{y+x\cdot y}{x}\qquad x\neq0$

Brugbart svar (0)

Svar #13
20. maj 2019 af AMelev

En lidt anden måde at skrive det samme på:
$\small f(x)=x\cdot e^x$ en løsning til differentialligningen $\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{y+x\cdot y}{x}\qquad x\neq0$ ⇔ $f '(x) = \frac{f(x)+x\cdot f(x)}{x}\Leftrightarrow f '(x) = \frac{x\cdot e^x+x\cdot x \cdot e^x}{x}\Leftrightarrow$
$1\cdot e^x+x\cdot e^x=\frac{x\cdot( e^x+x\cdot e^x)}{x}\Leftrightarrow$
$e^x+x\cdot e^x=e^x+x\cdot e^x\; \:\: \textup{Sandt!}$

Skriv et svar til: Bestem ligningen for tangenten til grafen for f i p(3,1)

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.