forskrift for parabel og integral

Du kan benytte, at forskriften kan skrives som A(x-r₁)(x-r₂),  hvor r₁ og r₂ er polynomiets rødder. A kan findes ved hjælp af formlen for toppuktet eller ved at indsætte koordinaterne til toppunktet.

Med udgangspunkt i toppunktet har vi at  svarer til  
Dermed har vi:
     

Og dermed er forskriften:
   f(x) = y_T + a·(x - x_T)²
   f(x) ≈ 3.1 - 2.344·(x - 1.15)²

Du kan anvende CAS som f.eks. Maple til at gøre det meget nemmere. Bemærk, at c=0, så du har kun et ligningssystem med to ukendte, nemlig a og b.

solve({a*1.85²+b*1.85=5.5,a*3.7²+b*3.7=0})

Løser du det får du a=-1.607012418 og b=5.945945946

Endvidere er c=0 som du får af a*0²+b*0+c=0.

Dermed er f(x)=-1.607012418x² + 5.945945946x

Du kan anvende det, som er angivet i #1.

#2: Ups, - værdier er aflæst forkert:

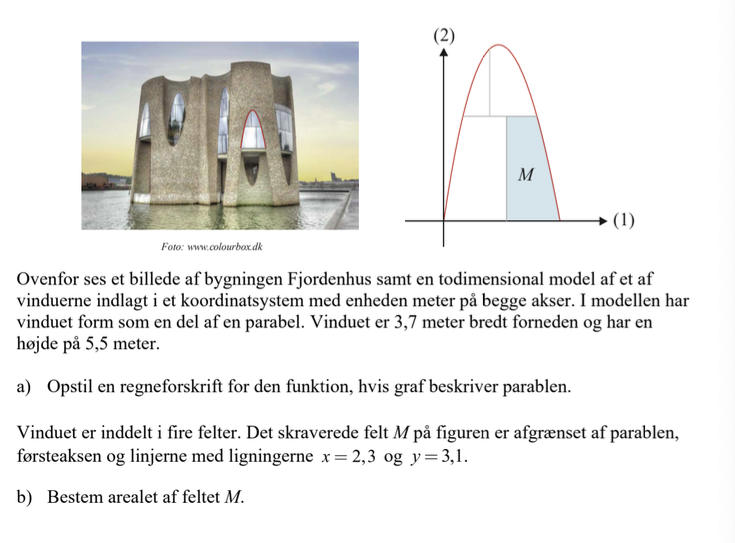
a)

b) 

#4

Kan du fortælle mig hvorfor du sætter hvilke tal ind i den solve command, da jeg gerne vil forstå det helt rigtigt til at kunne bruge det senere selv. Er nemlig ikke helt med i hvorfor det er de tal der sættes ind og hvorfro det er lige med de andre tal.

#5

Har du ikke byttet rundt på på linjerne ?

#4: Vinduets bredde (3.7 m) er afstanden mellem rødderne. Da rødder ligger symmestrisk omkring den akse hvorpå parablens toppunkt ligger, har toppunktet koordinaterne (den halve bredde, højde). Det giver to ligninger med to ubekendte:

#5: Angiv hvilke linjer du spørger til. Der er tre linjer.

#8 

Okay tak, jeg så forkert med linjerne så nvm.

i b)

Vil du forklare hvad de forskellige ting er der, er lidt forvirret over det?

#8

Mere præcist x1

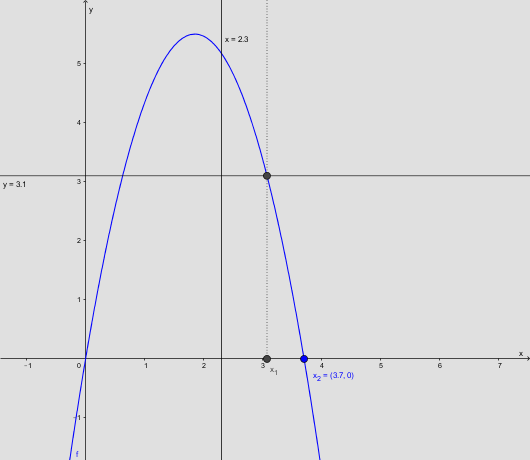
x₁ er løsningen på f(x) = 3.1 og x-koordinaten til det relevante skæringspunkt mellem linjen og parablen. Den skal bruges som den ene integrationsgrænse for integralet.