Matematik

mindst muligt

10. september 2019 af Nanna34 - Niveau: B-niveau

nogle har et bud?

skal man bruge montoniforhold?

Vedhæftet fil: Screenshot 2019-09-10 at 20.54.35.png

Brugbart svar (1)

Svar #1
10. september 2019 af ringstedLC

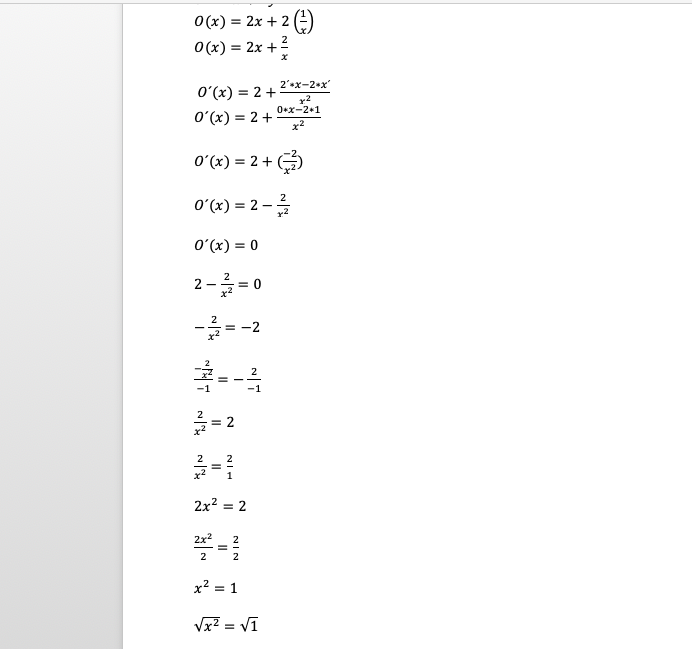
Du kan nøjes med at sætte diff.-kvotienten af en omkredsfunktion til nul:

$\begin{align*} x\cdot y &= 1\Leftrightarrow y=\tfrac{1}{x} \\ O(x)&=2x+\tfrac{2\,\cdot 1}{x}\;,\;x\neq 0 \\ O'(x) &=\;?= 0 \\ x &=\;? \end{align*}$

Rigtigt løst skal det gerne vise sig, at et kvadrat har det største areal i forhold til omkredsen.

Svar #2
11. september 2019 af Nanna34

#1

Du kan nøjes med at sætte diff.-kvotienten af en omkredsfunktion til nul:

$\begin{align*} x\cdot y &= 1\Leftrightarrow y=\tfrac{1}{x} \\ O(x)&=2x+\tfrac{2\,\cdot 1}{x}\;,\;x\neq 0 \\ O'(x) &=\;?= 0 \\ x &=\;? \end{align*}$

Rigtigt løst skal det gerne vise sig, at et kvadrat har det største areal i forhold til omkredsen.

hvad gøre jeg nu så jeg får x til 1

Vedhæftet fil:Screenshot 2019-09-11 at 20.47.32.png

Brugbart svar (0)

Svar #3
11. september 2019 af ringstedLC

Brug at:

$\begin{align*} \sqrt{a^2} &= a \\ \sqrt{1} &= \sqrt{1^2} \end{align*}$

Skriv et svar til: mindst muligt

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.