Geometri og binære ligningssystemer

#0. Se evt. https://www.studieportalen.dk/forums/thread.aspx?id=1915400.

#1
#0. Se evt. https://www.studieportalen.dk/forums/thread.aspx?id=1915400.

Du er godt nok ikke til særlig megen hjælp, Soeffi.

Mht. spørgsmålet, så indsæt a=0 i totalmatricen, og få den på trappeform. Du skulle gerne få ligningen for en yz-plan.

Okay, så får man en matrice som lyder <1, 0, 0, 0; 0, 0, 0, 0; 0, 0, 0, 0; 0, 0, 0, 0>. Hvor der så kun er en fast parameter altså x1 = 0, og så har man to frie parametre hvor 4 og -4 kan ingå? Hvilket giver en samlet parameterfremstilling som er: (x, y, z) = (0, 0, 0) + t*(0, 1, 0) + s*(0, 0, 1). Hvor t er x2 og s er x3. Når man så sætter 4 og -4 ind på de to frie parametre får man to punkter som er (0, 4, -4) og (0, -4, 4).

Eller har jeg misforstået opgaven?

Det er rigtigt, men der er ingen grund til at opstille en parameterfremstilling. Du ved jo at det er en yz-plan.

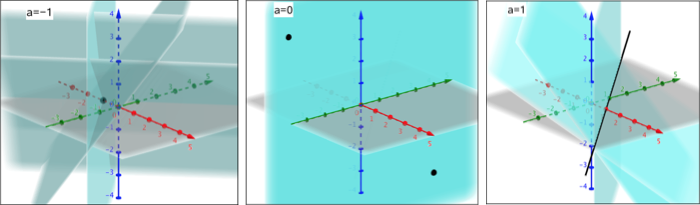
#0. Der er tre tilfælde med hensyn til a:

1) a = -1 ⇒ fælllesmængden for planerne er et punkt

2) a = 0 ⇒ fælllesmængden for planerne er et plan

3) a = 1 ⇒ fælllesmængden for planerne er en linje

Man skal så undersøge i hvert tilfælde, om punkter med koordinaterne -4 og 4 kan optræde i fællesmængden.

Lavet i Geogebra:

#5...for andre værdier af a, så er fællesmængden af punkterne i planerne den tomme mængde.

#0. Løsning ved reduktion af matrix. 

Hvis man reducerer matricen for ligningssystemet i CAS, så får man enhedsmatricen. Det skyldes, at CAS ikke tager hensyn til, om der divideres med 0. Hvis man vil reducere uden at dividere, så får man:

Denne matrix kan reduceres yderligere ved at dividere med henholdsvis a² - a, a og a - a³ i række 2, 3 og 4 for derefter at gange række 2 og 4 med a og trække dem fra række 1. Dette forudsætter dog, at a er forskellig fra -1, 0 og 1, da man ellers ville dividere med 0.

a forskellig fra -1, 0 og 1:
Fjerde række giver ligningen: 0·x + 0·y + 0·z = a - a³ ≠ 0, hvilket ikke kan lade sig gøre, og planerne har dermed ikke nogen fælles punkter.

a = -1:

Dette giver ligningerne:  x - y = -1, 2y = 0, -z = 0 og 0 = 0 ⇒ x - y = -1, y = 0 og z = 0 ⇒ x = -1, y = 0 og z = 0.
Dvs. planerne har det fælles punkt: (x,y,z) = (-1,0,0).

a = 0:

 

Dette giver planen x = 0, dvs. YZ-planen som fællesmængde. Det viser sig, at kun denne fællesmængde rummer punkter med koordinatene -4 og 4.

a = 1:

Dette giver ligningerne: x + y = 1 og z = 0. Dette ses, at være linjen x + y = 1 i XY-planen (z = 0).
Parameterfremstillingen kan laves ved forsøgsvis at sætte y = 0 hvilket giver punktet (x,y,z) = (1,0,0) på linjen. Retningsvektoren kan findes som krydsproduktet af planernes normalvektorer. Disse findes ved at opskrive de fulde ligninger for planerne: 1·x + 1·y + 0·z = 1 og 0·x + 0·y + 1·z = 0.
Normalvektorerne er n = (1,1,0) og m = (0,0,1). n × m = (1,1,0) × (0,0,1) = (1,-1,0).
Dvs. parameterfremstillingen bliver: (x,y,z) = (1,0,0) + t·(1,-1,0), t ∈ R.