Matematik

cirklen

21. januar 2020 af lektiehjælp0012 - Niveau: A-niveau

nogen der kan hjælpe med vedhæftede opgave

Svar #1
21. januar 2020 af lektiehjælp0012

Vedhæftet fil:Skærmbillede 2020-01-21 kl. 17.15.19.png

Brugbart svar (1)

Svar #2
21. januar 2020 af peter lind

Brugbart svar (1)

Svar #3
21. januar 2020 af peter lind

a) brug formel 75 side 15 i din formelsamling

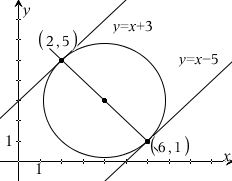
b) Jeg kalder tværvektoren til (1, 1) for v. Afsæt vektoren til ±v/|v| med længden r/2 ud fra centrum. Det giver de angivne punkter

Kommemtar til opgaven: Det er sjusk at have r i to forskellige betydninger

Svar #4
21. januar 2020 af lektiehjælp0012

men hvad hvis man løser den med værktøjet CAS

Brugbart svar (1)

Svar #5
21. januar 2020 af peter lind

Jeg kender ikke dit CAS værktøj, så der kan jeg ikke hjælpe dig. Spørgsmål a kan du i hvert fald ikke klare med CAS og jeg tvivler også på at CAS kan være til nogen hjælp til b.

Brugbart svar (1)

Svar #6
21. januar 2020 af AMelev

Jeg forstår ikke helt anvisningen i #3.

Alternativer:
Radiuslinjen n gennem C vinkelret på tangenterne skærer cirklen i røringspunkterne
1) Parrameterfremstilling - Måske lettest
Bestem parameterfremstillingen for radiuslinjen n - retninggsvektoren er tværvektoren til tangenternes retningsvektor (FS side 12 (57)) . Indsæt i cirklens ligning og løs mht. t. Indsæt t-værdierne i parameterfremstillingen.

2) Ligning
Bestem ligningen for radiusligningen n (FS side 15 (71)) og isoler y. Indsæt i cirklens ligning og løs mht. x. Indsæt i det isolerede y-udtryk.

Vedhæftet fil:Udklip.JPG

Brugbart svar (1)

Svar #7
21. januar 2020 af mathon

$\small \begin{array}{lllll} \textup{R\o ringspunkter}&R_1\textup{ og }R_2\\\\&\overrightarrow{OR}=\overrightarrow{OC}\mp r\cdot \frac{\overrightarrow{v}}{\left | \overrightarrow{v} \right |}\\\\&\overrightarrow{OR}=\overrightarrow{OC}\mp \frac{r}{\left | \overrightarrow{v} \right |}\cdot \overrightarrow{v}\\\\&\overrightarrow{OR}=\begin{pmatrix} 4\\3 \end{pmatrix}\mp \frac{\sqrt{8}}{\sqrt{2}}\cdot \begin{pmatrix} -1\\1 \end{pmatrix}\\\\&\overrightarrow{OR}=\begin{pmatrix} 4\\3 \end{pmatrix}\mp \begin{pmatrix} -2\\2 \end{pmatrix}\\\\\\&\overrightarrow{OR}_1=\begin{pmatrix} 4\\3 \end{pmatrix}- \begin{pmatrix} -2\\2 \end{pmatrix}=\begin{pmatrix} 6\\1 \end{pmatrix}\\\\\textup{dvs}&R_1=(6,1)\\\\&\overrightarrow{OR}_2=\begin{pmatrix} 4\\3 \end{pmatrix}+ \begin{pmatrix} -2\\2 \end{pmatrix}=\begin{pmatrix} 2\\5 \end{pmatrix}\\\\\textup{dvs}&R_2=(2,5) \end{array}$

Brugbart svar (1)

Svar #8
21. januar 2020 af AMelev

Ad #4 Hvilket CAS-værktøj benytter du?
Du kan bruge CAS til at løse ligningerne og nok også til at løse opgaven geometrisk, men i hvert fald i Nspire er det ret kringlet. Jeg ved ikke, hvordan det ser ud i Geogebra eller Maple, men jeg vil tro, det er lettere at løse opgaven analytisk med en af ovenstående metoder.

Brugbart svar (1)

Svar #9
21. januar 2020 af ringstedLC

#4
men hvad hvis man løser den med værktøjet CAS

CAS er ikke ét værktøj, så når du spørger om hjælp til din CAS, bør det angives hvilket program, du anvender.

a) I GeoGebra (et CAS-program) indtastes: cirkel((4,3), sqrt(8))

b) De to tangenter er rette linjer i distancen = r fra C som er parallelle med vektor r. Brug at:

$\begin{align*} m_1\text{ og }m_2:y &= ax+b \\ \overrightarrow{r} &= \binom{1}{1}\Rightarrow a=\;? \\ \left.\begin{matrix}dist(C,\,m_1) \\ dist(C,\,m_2) \end{matrix}\right\}=r=\sqrt{8} &= \frac{|a\,C_x+b-C_y|}{\sqrt{a^2+1}} \Rightarrow b=\left\{\begin{matrix}b_{m_1}\Rightarrow y_{m_1}=ax+b_{m_1} \\ b_{m_2}\Rightarrow y_{m_2}=ax+b_{m_2} \end{matrix}\right. \\ \left (x-C_x \right )^2+\left ( y-C_y \right )^2 &= \left (\sqrt{8} \right )^2 \\ \Rightarrow y=\,...\, &= \left\{\begin{matrix}y_{m_1} \\ y_{m_2} \end{matrix}\right.\;,\;y \text{ kan isoleres i cirklens ligning, ogs\aa\;med CAS}\\ x &= \left\{\begin{matrix}x_1\\x_2 \end{matrix}\right. \\ y &= \left\{\begin{matrix} y_1=ax_1+b_{m_1}\\y_2=ax_2+b_{m_2} \end{matrix}\right\}\Rightarrow \left\{\begin{matrix}R_1=(x_1, y_1) \\ R_2=(x_2,y_2) \end{matrix}\right. \end{align*}$

Dette kan laves i CAS, hvis man holder styr på sine definitioner. Og facit har du i #7.

Svar #10
22. januar 2020 af lektiehjælp0012

mange tak alle sammen

Skriv et svar til: cirklen

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.