Matematik
Jordens radius
Hej SP
Jeg sidder her og funker lidt med denne opgave, men ved ikke helt hvad jeg skal gøre. Opgaven lyder:
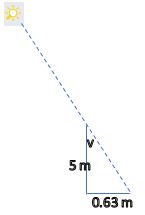
En 5 meter høj obelisk kaster en skygge der er 0,63 meter.
Beregn den vinkel som solens stråler afviger fra lodret.
Jeg ved ikke hvordan jeg skal udregne det eller hvilken formel jeg skal bruge. Håber nogen kan hjælpe. Og er det 7,2?
På forhånd tak!
Svar #1
14. februar 2020 af Festino
Da obelisken er vinkelret på underlaget, har vi en retvinklet trekant, hvor vi kender begge kateter. I en retvinklet trekant er tangens til en af de spidse vinkler lig med modstående katete divideret med hosliggende katete.
Ja, svaret er .
Svar #2
14. februar 2020 af KageSpiseren
#1Da obelisken er vinkelret på underlaget, har vi en retvinklet trekant, hvor vi kender begge kateter. I en retvinklet trekant er tangens til en af de spidse vinkler lig med modstående katete divideret med hosliggende katete.
Ja, svaret er
.
Så hvordan vil beregningen se ud helt præcist? for jeg tror ikke det er ellers har jeg misforstået.
Svar #4
14. februar 2020 af KageSpiseren
#3Nej, det er
,
idet
.
Forstår ikke helt.
Er det ikke også bare muligt at bruge de værdier jeg allerede har til at finde sider og vinkler:
A = 90 grader
B=?
C=?
a=?
b= 5
c= 0,63
også bruger jeg sinus og cosinus relationerne eller er det forkert af mig?
Svar #5
14. februar 2020 af Festino
Du kunne godt starte med at finde ved hjælp af Pythagoras', og så bruge cosinusrelationen, men det er lidt mere besværligt. Man bruger typisk sinus- og cosinusrelationen ved trekanter, der ikke er retvinklede.
Svar #6
15. februar 2020 af KageSpiseren
#5Du kunne godt starte med at finde
ved hjælp af Pythagoras', og så bruge cosinusrelationen, men det er lidt mere besværligt. Man bruger typisk sinus- og cosinusrelationen ved trekanter, der ikke er retvinklede.
men man kan stadig bruge relationerne i en retvinklet, ikke også?
Svar #7
15. februar 2020 af AMelev
#6
Jo, men det vil være ud fra devisen "Hvorfor gøre noget let, når det kan gøres besværligt?"
Svar #8
15. februar 2020 af KageSpiseren
#7#6
Jo, men det vil være ud fra devisen "Hvorfor gøre noget let, når det kan gøres besværligt?"
Jeg forstod stadig ikke det med tan 0,63/5 også tan (v). Hvordan giver det 7,2?
Derfor valgte jeg sinus og cosinus
Svar #10
16. februar 2020 af ringstedLC
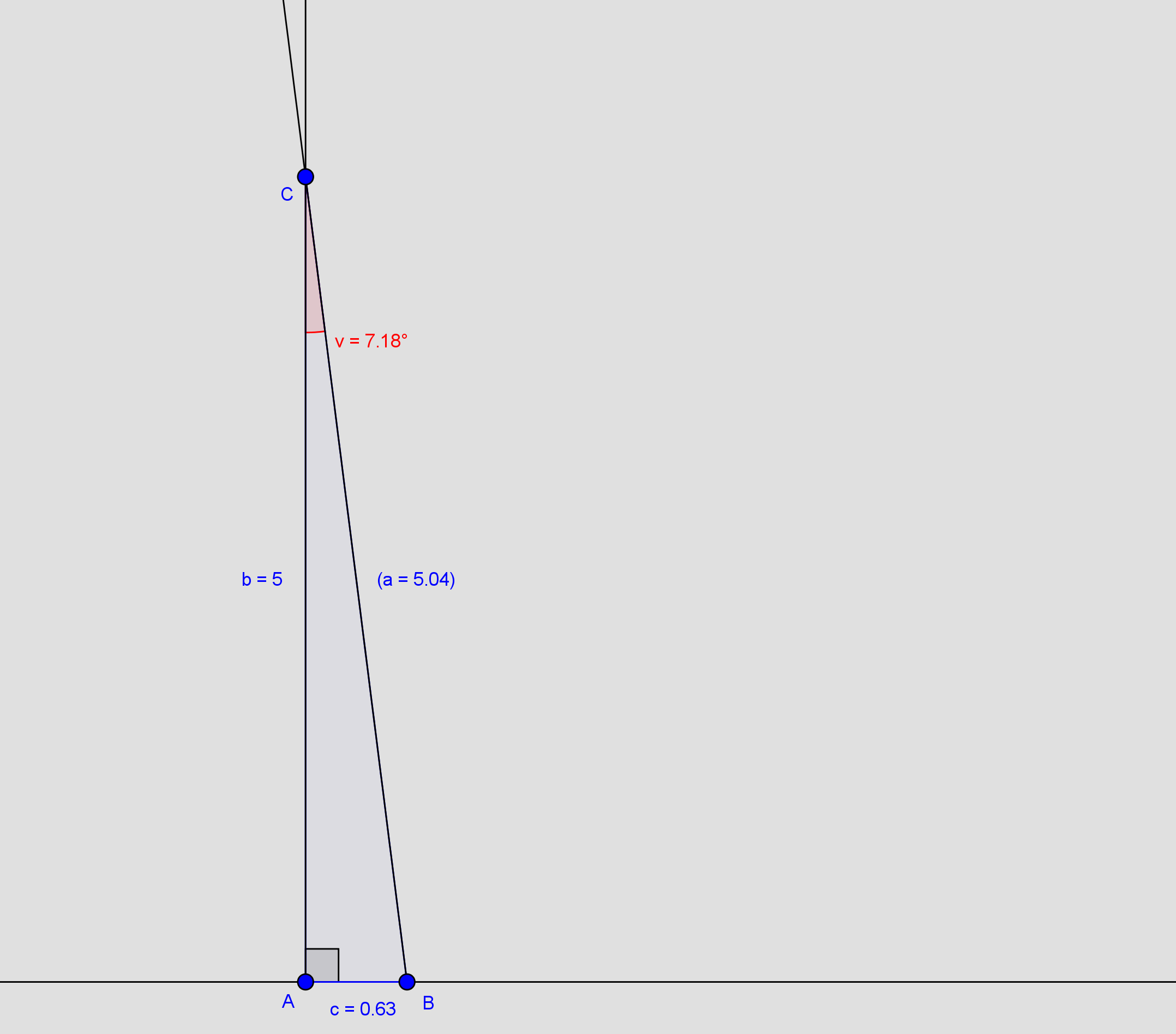
#6: Sinus- og cosinusrelationerne for den vilkårlige trekant gælder (selvfølgelig) også den retvinklede trekant. Men da én vinkel i den retvinklede er kendt, har vi omskrevet dem og tilføjet tangensrelationen:
Med sinusrelationen:
Med cosinusrelationen:
Svar #11
16. februar 2020 af KageSpiseren
#10#6: Sinus- og cosinusrelationerne for den vilkårlige trekant gælder (selvfølgelig) også den retvinklede trekant. Men da én vinkel i den retvinklede er kendt, har vi omskrevet dem og tilføjet tangensrelationen:
Med sinusrelationen:
Med cosinusrelationen:
Forstår bedre nu. Tak for det. Så hvordan vil I/du definere hvornår man bruger tangens?
Svar #12
16. februar 2020 af AMelev
#11 I retvinklede trekanter, hvor de to kateter er involveret, dvs.
1) De to kateter kendes, og en vinkel skal bestemmes, eller
2) En katete og en vinkel er kendt, og den anden katete skal bestemmes.
Svar #13
16. februar 2020 af ringstedLC
#11: Bare et lille "suk", - undlad at bruge citérfunktionen, når du bare vil svare på et indlæg. Når nu nogen af os, heriblandt undertegnede, laver sådan nogle forfærdelig lange svar m. figurer m.m., mistes overblikket.
Og hold så fast i trigonometrien i retvinklede trekanter. Det er Folkeskolepensum og du går i HTX på A-niveau.
Svar #14
16. februar 2020 af KageSpiseren
Det beklager jeg for. Det vil ikke gentages.
Det rigtigt nok det folkeskolepensum, men jeg har vel ikke fået samme profesionelle undervisning som du har. Tværtimod har folkeskole slet ikke hjulpet mig med noget da jeg selv har prøvet at lære mig selv ting som ikke indgik i der hvor jeg gik i folkeskole, men det forstået. Skal nok prøve at holde fast i trigonometrien i retvinklede trekanter siden jeg går på HTX A-niveau.
Svar #15
16. februar 2020 af ringstedLC
#14: Det har du vist nævnt før. Men tiden går, lige om lidt er du en tredjedel henne mod eksamen og der kommer flere og flere nye emner som kræver at det elementære er iorden. Hvis du er en "slider", og det tror jeg, kan du nå at indhente det forsømte. Eks.: Når du slår op i FS for at finde den formel vedr. trekanten som lige er blevet "væk", så tving dig selv til at prøve en af de andre formler. Der er så mange sammenhænge og derfor formler omkring trekanter og du bør være nogenlunde hjemme i dem alle.
I #0 har du jo faktisk det rigtige svar. Men det var så med cos/sin eller...
Svar #16
16. februar 2020 af KageSpiseren
Er dog ikke en slider, men har bare haft massere af udfordringer i matematik og derfor er det jeg laver så mange forumindlæg. Nogen har været svære for mig, mens nogen har været lette for andre og omvendt. Og selvfølgelig forstår jeg at din tid er dyrebar og jeg er yderst taknemlig at du har svaret på nærmest hver eneste af de forumindlæg jeg har oprettet. Men skal nok fremover tage mig lidt mere sammen end det jeg allerede er.
Ja dsv var det med cos/sin men som du havde sat op i #10 så var jeg bange for fejl. Men er glad for at have kendskab til tangens nu takket være jer!
Svar #17
16. februar 2020 af ringstedLC
Og selvfølgelig forstår jeg at din tid er dyrebar og jeg er...
Det skal du slet ikke spekulere over. Jeg arbejder for min egen fornøjelses skyld.
Det, du skal spekulere over, det er, om du virkelig vil det her. For når din Folkeskole-matematik har så været så dårlig som du skriver, så bliver det et slid at følge med.
Go' arbejdslyst.
Skriv et svar til: Jordens radius
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.