Matematik

Funktioner af to variable, bestem k så f(x,y) ikke har nogen løsning

01. marts 2020 af chiladak - Niveau: A-niveau

Jeg har vedhæftet opgaven, det er b) det drejer sig om.

Er der nogen der kan fortælle mig hvorledes jeg løser denne? :)

Vedhæftet fil: Skærmbillede 2020-03-01 kl. 12.37.57.png

Brugbart svar (0)

Svar #1
01. marts 2020 af mathon

Brugbart svar (0)

Svar #2
01. marts 2020 af mathon

b)
For hvilke værdier af k, kan f(x,y) = k ikke være ligningen for en cirkel?

Svar #3
01. marts 2020 af chiladak

Jeg tror ikke helt hvordan jeg løser dette? jeg har omskrevet funktion til cirklens ligning (x + 0)² + (y - 1)² = 3², skal jeg benytte dette?

Brugbart svar (2)

Svar #4
01. marts 2020 af mathon

$\small \begin{array}{lllll}\textup{i a})\\&(x-0)^2+(y-1)^2=6+3\\\\\\\textup{i b})\\&\underset{\geq 0}{\underbrace{(x-0)^2+(y-1)^2}}=k+3\\\\&\textup{bestem de v\ae rdier af k, hvor ovenst\aa ende ligning \textbf{ikke} har nogen reel l\o sning.} \end{array}$

Svar #5
01. marts 2020 af chiladak

Okay det giver mening, dog er jeg lidt i tvivl, hvorledes udregner jeg nu denne, skal jeg solve når nu jeg skal inddrage >0

Brugbart svar (0)

Svar #6
01. marts 2020 af mathon

Hvordan med reel løsning, hvis k < -3?

Svar #7
01. marts 2020 af chiladak

Jeg tror jeg misforstår dig, er ikke helt med på din fremgangsmåde?

Brugbart svar (4)

Svar #8
01. marts 2020 af ringstedLC

$\begin{align*} f(x,y)=k &= x^2+(y-1)^2-3 \\ k+3 &= x^2+(y-1)^2 \\ r^2=k+3 &= x^2+(y-1)^2 \\ r=\sqrt{k+3}&\geq0\text{ (giver en cirkels ligning)} \\ k+3&\geq0 \\ k&\geq-3\Rightarrow k<-3 \text{ (giver \textbf{ikke} en cirkels ligning)} \end{align*}$

Brugbart svar (1)

Svar #9
01. marts 2020 af Soeffi

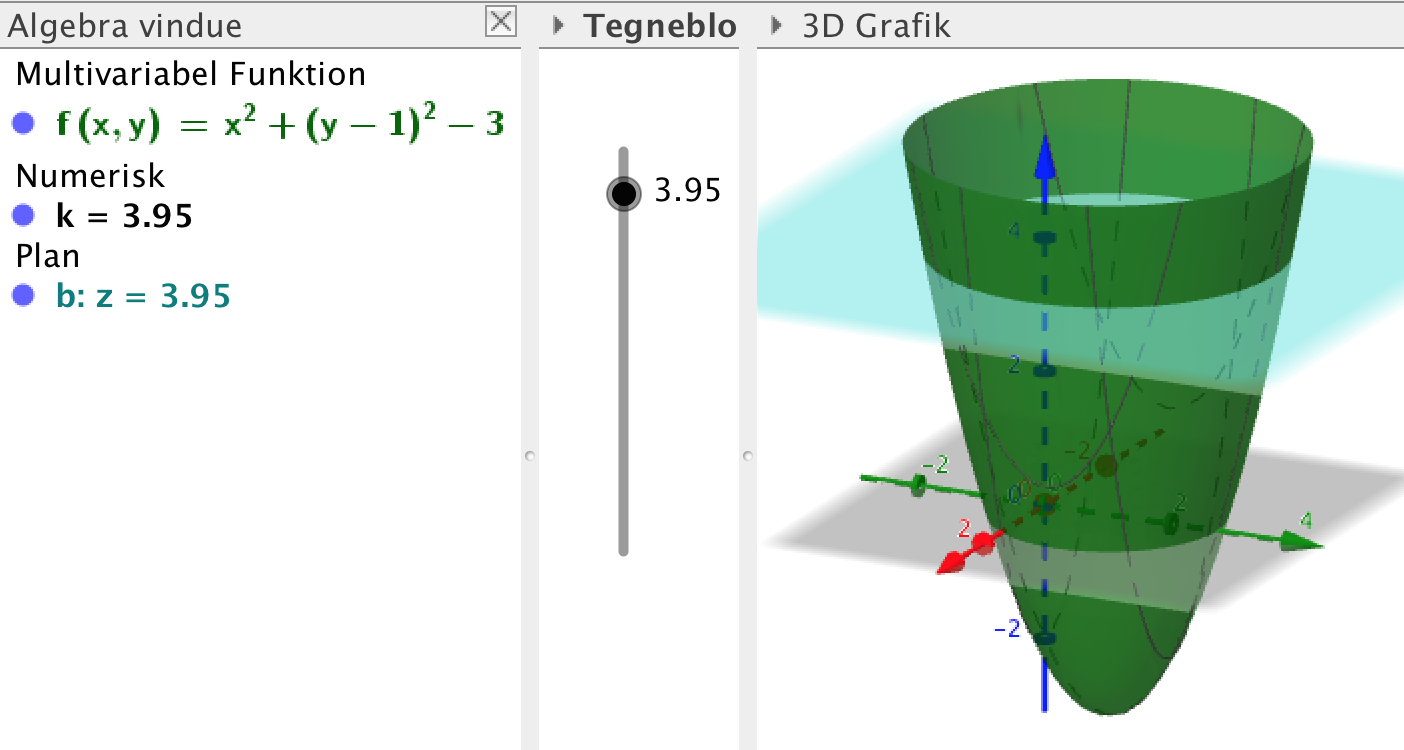
#0. Niveaukurven f(x,y) = k svarer til skæringen mellem grafen for f og planen z = k som vist (med k = 3,95 som eksempel).

Vedhæftet fil:Skærmbillede 2020-03-01 kl. 17.48.11.png

Svar #10
02. marts 2020 af chiladak

Tak alle, jeg forstår det nu:)

Skriv et svar til: Funktioner af to variable, bestem k så f(x,y) ikke har nogen løsning

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.