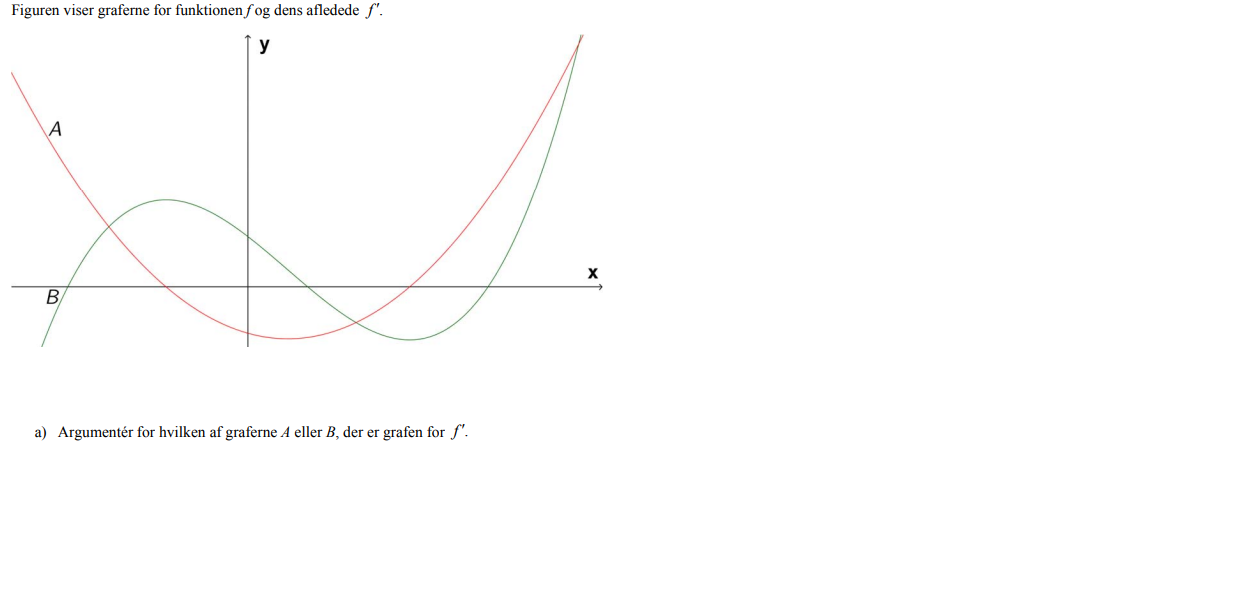
Matematik
Hvad tilhører grafen?
Hej.
Jeg forstår ikke helt, hvordan man løser disse slags opgaver? :)
Svar #3
26. maj 2020 af mikkel981
Den information forstår jeg ikke helt, jeg ved dog hvad lokalt maksimum eller minimum betyder.
Men "dens aflede er 0" det udtryk forstår jeg ikke helt.. Unskyld jeg er krævende.
Svar #4
26. maj 2020 af Jones2929
#3Den information forstår jeg ikke helt, jeg ved dog hvad lokalt maksimum eller minimum betyder.
Men "dens aflede er 0" det udtryk forstår jeg ikke helt.. Unskyld jeg er krævende.
Hvis funktionen f(x) har et lokalt maksimum eller minimum, så er funktionen f'(x) = 0 (den skærer x - aksen).
Vi ser, at B skærer x - aksen, når A har lokalt maksimum og minimum. Hvad siger det for opgaven?
Svar #5
26. maj 2020 af mikkel981
At grafen B er f '
Jeg kan ikke rigtig se det der (Hvis funktionen f(x) har et lokalt maksimum eller minimum, så er funktionen f'(x) = 0 (den skærer x - aksen). )
Har du mulighed for at tegne det på tegningen, sry.
Svar #6
26. maj 2020 af peter lind
Det har jeg ikke; men jeg kan forklare det. Den røde har et minimum og den grønne skærer x-aksen 3 steder
Den grønne har 2 ekstemaer og se selv efter om det passer med at den grønnes skæring med x-aksen
Svar #7
26. maj 2020 af Jones2929
#5At grafen B er f '
Jeg kan ikke rigtig se det der (Hvis funktionen f(x) har et lokalt maksimum eller minimum, så er funktionen f'(x) = 0 (den skærer x - aksen). )
Har du mulighed for at tegne det på tegningen, sry.
Nej. Det er A, som er f' (jeg lavede dog en lille fejl i min originale besked. Undskyld :) )
Lokalt maksimum og minimum: B har et lokalt minimum lidt før (0;0) og et lokalt maksimum lidt efter (0;0).
Nu ved jeg ikke hvad det nøjagtige koordinat er, så jeg skriver bare "x"
Den vokser fra , aftager fra
og vokser i
Svar #8
26. maj 2020 af mikkel981
Nu har jeg markeret den grønne 2 ekstremaer og skæringer med x-aksen, samt den røde grafs minimum.
Jeg kan bare ikke se, hvordan man aflæser hvilken graf det er.
Det ser ud til at jeg dumper i morgen når jeg ikke kan løse så "nemme" opgaver
Svar #9
26. maj 2020 af Jones2929
#8Nu har jeg markeret den grønne 2 ekstremaer og skæringer med x-aksen, samt den røde grafs minimum.
Jeg kan bare ikke se, hvordan man aflæser hvilken graf det er.
Det ser ud til at jeg dumper i morgen når jeg ikke kan løse så "nemme" opgaver
Hej igen. Jeg lavede en lille fejl. Jeg forvekslede A og B i besked 4. Tjek besked 7 og min vedhæftning
Jeg lavede en lille fejl
Svar #10
26. maj 2020 af mikkel981
Ah nu kan jeg se, hvordan man aflæser det.
Mange tak Jones for din tegning og tak Peter for hjælpen.
Svar #11
26. maj 2020 af Jones2929
#10Ah nu kan jeg se, hvordan man aflæser det.
Mange tak Jones for din tegning og tak Peter for hjælpen.
Intet problem. Jeg havde selv ret svært ved monotoniforhold og differentielregning i starten. Du skal nok klare den i morgen. Selv forstår jeg ikke, hvorfor disse opgaver er en del af opgaverne uden hjælpemidler. Jeg synes selv, at de er lidt i den svære ende for opgaver uden hjælpemidler
Skriv et svar til: Hvad tilhører grafen?
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.