Max area of rectangle

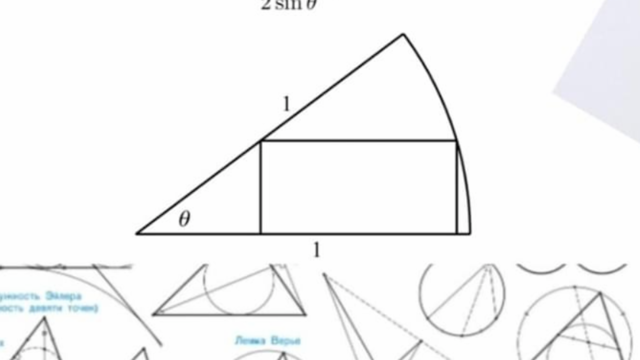
26. maj 2020 af janhaa - Niveau: Universitet/Videregående

A rectangle is inscribed in a sector of a circle of radius 1, see picture below. The angle in the sector is given,

$\theta,\\ where: 0< \theta \leq \pi/2.$

Show that the max possible area for the rectangle is:

$\frac{1-\cos(\theta)}{2\sin(\theta)}$

some hints or a solution?

(and yes I have tried).

Vedhæftet fil: sirkel-sector-rektangel.PNG

Brugbart svar (1)

Svar #1
26. maj 2020 af Mathias7878

Math Stack Exchange?

- - -

Brugbart svar (0)

Svar #2
26. maj 2020 af Soeffi

Brugbart svar (1)

Svar #3
26. maj 2020 af Soeffi

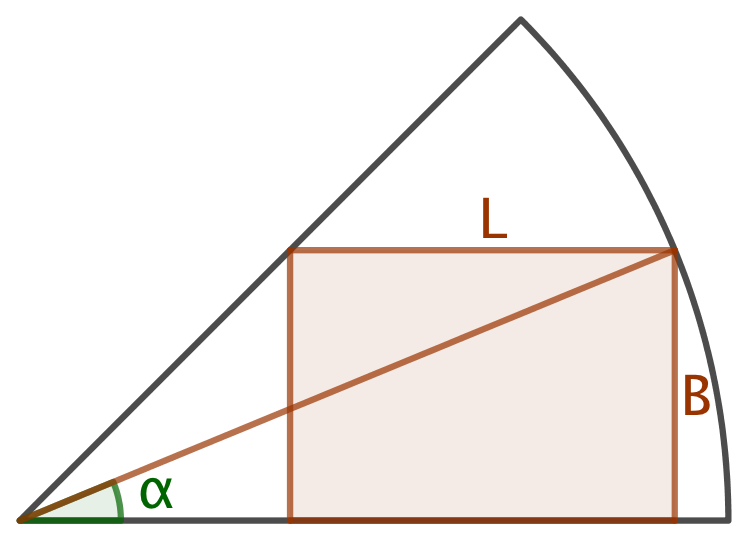
#0. Se tegningen nedenfor. Jeg får: Areal = L·B = (1 - cos(α) + sin(α)/tan(θ))·sin(α). Tilsyneladenden er der maksimum for A ved α = θ/2 (?)

Vedhæftet fil:Untitled.png

Brugbart svar (1)

Svar #4
27. maj 2020 af Soeffi

#3. Rettelse: B = sin(α), L = cos(α) - 1/tan(θ) = cos(α) - cos(θ)/sin(θ)
Areal = B·L = sin(α)·(cos(α) - cos(θ)/sin(θ))

Brugbart svar (0)

Svar #5
27. maj 2020 af Soeffi

#4. Undskyld: L = cos(α) - sin(α)/tan(θ)
Areal = sin(α)·(cos(α) - sin(α)·cos(θ)/sin(θ)), 0<α<θ<π

Svar #6
27. maj 2020 af janhaa

I got answers from math Stackexchange

Flinke folk der :=)

Brugbart svar (0)

Svar #7
28. maj 2020 af Soeffi

#5. A(α,θ) = sin(α)·(cos(α) - sin(α)·cos(θ)/sin(θ)) = (1/2)·(sin(2α)-(1-cos(2α))·cot(θ)), 0<α<θ<π/2.

A'(α,θ) = sin(2α)·(cot(2α)-cot(θ)), 0<α<θ<π/2.

A'(α,θ) = 0 ⇒ α = 0 ∨ α = θ/2, 0<α<θ<π/2. Maksimum ved α = θ/2.

A(θ/2,θ) = (1/2)·tan(θ/2) = (1-cos(θ))/sin(θ).

Skriv et svar til: Max area of rectangle

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.