Matematik

Linjens skæring i cirkel

29. maj 2020 af Ladora (Slettet) - Niveau: B-niveau

Hej, jeg har denne opgave:

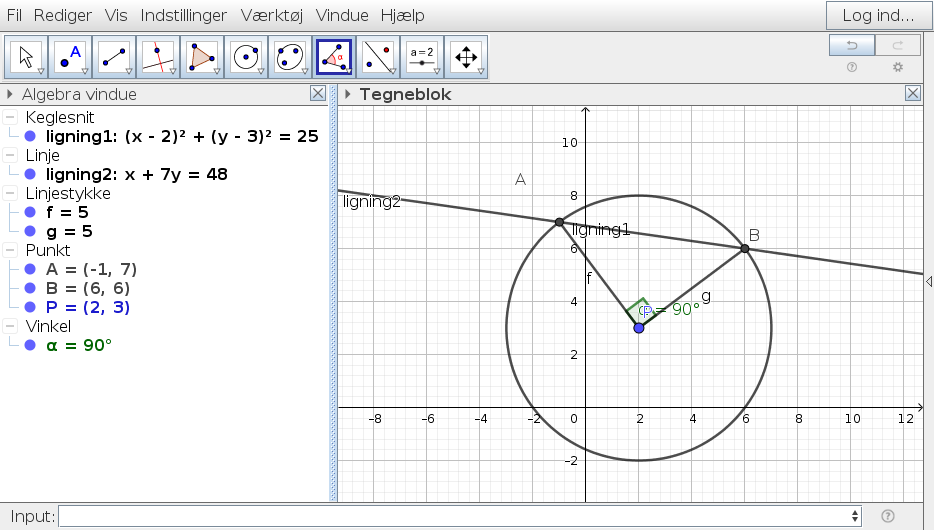
Har lavet a), hvor afstanden er 3.54 og b), hvor cirklens ligning er (x - 2)² + (y - 3)² = 25

Men jeg er i tvivl om opgave c), har læst om det, men forstår det ikke :(

Brugbart svar (1)

Svar #1
29. maj 2020 af StoreNord

A, B og P danner en retvinklet trekant med kateter=radius og AB som hypotenuse.

Brugbart svar (1)

Svar #2
29. maj 2020 af StoreNord

Vedhæftet fil:Skærmbillede fra 2020-05-29 15-32-16.png

Brugbart svar (1)

Svar #3
29. maj 2020 af StoreNord

Svar #4
29. maj 2020 af Ladora (Slettet)

Men jeg skal lave en vektor, som bestemmer ->AB

Svar #5
29. maj 2020 af Ladora (Slettet)

Og lave det med beregning :(

Brugbart svar (1)

Svar #6
29. maj 2020 af mathon

Vektoren kan du opstille med kendskab til de skæringspunkters koordinater.

Svar #7
29. maj 2020 af Ladora (Slettet)

Hvordan finder jeg koordinaterne med beregning? :o

Svar #8
29. maj 2020 af Ladora (Slettet)

Har fundet punkternes koordinater med beregning, hvordan laver jeg så en vektor ud af det? :o A = -1,7 og B = 6, 6

Vedhæftet fil:Skærmbillede 2020-05-29 kl. 15.56.27.png

Brugbart svar (1)

Svar #9
29. maj 2020 af mathon

$\small \begin{array}{llll} \textup{linjen:}&x=48-7y\\ \textup{som indsat i}\\&(x-2)^2+(y-3)^2=5^2\\ \textup{giver:}\\& (48-7y)^2+(y-3)^2=25\\\\& 49y^2-672y+2304+y^2-6y+9=25\\\\& 50y^2-678y+2288=0\\\\& y=\left\{\begin{matrix} \frac{339-\sqrt{521}}{50}\\ \\\frac{339+\sqrt{521}}{50} \end{matrix}\right. \end{array}$

Brugbart svar (2)

Svar #10
29. maj 2020 af StoreNord

#8
Så trækker du x-koordinaterne fra hinanden, og y-koordinaterne fra hinanden.

Men der står ikke noget i opgaven om en vektor. (kun hvis jeg tar briller på)
Du kan bare bruge Afstands-formelen (Pythagoras).

Svar #11
29. maj 2020 af Ladora (Slettet)

Skal det være en normalvektor eller retningsvektor? er svaret på c) så $\binom{7}{-1} eller \binom{-1}{7}$

Brugbart svar (1)

Svar #12
29. maj 2020 af mathon

$\small \small \begin{array}{llll} & y=\left\{\begin{array}{lll} \frac{339-\sqrt{521}}{50}\\&&\textup{med koordinerede x-v\ae rdier} \left\{\begin{matrix} \frac{27+7\cdot \sqrt{521}}{50}\\ \frac{27-7\cdot \sqrt{521}}{50} \end{matrix}\right. \\ \frac{339+\sqrt{521}}{50}\end{array}\right. \end{array}$

Svar #13
29. maj 2020 af Ladora (Slettet)

Hvordan finder jeg afstanden? :o

Brugbart svar (1)

Svar #14
29. maj 2020 af StoreNord

https://www.webmatematik.dk/lektioner/matematik-b/geometri/afstandsformlen

Svar #15
29. maj 2020 af Ladora (Slettet)

Tusind tak, gutter! Afstanden er 7.07, hvis jeg ikke tager fejl? Så er svaret på c) 7.07 ikke?

Brugbart svar (1)

Svar #16
29. maj 2020 af mathon

$\small \overrightarrow{AB}=\begin{pmatrix} \frac{339-\sqrt{521}-(339+\sqrt{521})}{50}\\\\ \frac{339-\sqrt{521}-(339+\sqrt{521})}{50} \end{pmatrix}$

Svar #17
29. maj 2020 af Ladora (Slettet)

Er svaret ikke 7.07? :o skal aflevere om 28 min, og er meget forvirret :(

Brugbart svar (1)

Svar #18
29. maj 2020 af Eksperimentalfysikeren

A og B ligger begge på linien, så AB er en retningsvektor. Du har ikke brug forat vide, at det er en vektor, du skal finde længden af liniestykket AB.

Tegn den radius, der står vinkelret på linien. Den skærer AB i midten. Skæringspunktet kaldes M. Da vinkel PMA er ret, er trekant PAM retvinklet. Du kender PA, som er radius, og PM, som har den længde, du regnede ud i a. Så bruger du Pythagoras til at finde den resterende korte AM. Du skalså lige huske, at det kun er halvdelen af AB.

#1 Hvor har du fra, at trekant ABP er retvinklet?

Brugbart svar (1)

Svar #19
29. maj 2020 af Eksperimentalfysikeren

Det kommer jeg ikke til 7,06.

Svar #20
29. maj 2020 af Ladora (Slettet)

Nu er jeg endnu mere forvirret :((( skal jeg i c) bare finde længden af linjestykket AB? For det er vel 7.07?

Forrige 1 2 Næste

Der er 32 svar til dette spørgsmål. Der vises 20 svar per side. Spørgsmålet kan besvares på den sidste side. Klik her for at gå til den sidste side.