Matematik
Rundkørslen
Hej alle
Jeg sidder med en opgave som har drillet mig nok så håber at nogle det vil give tid og hjælpe lidt.
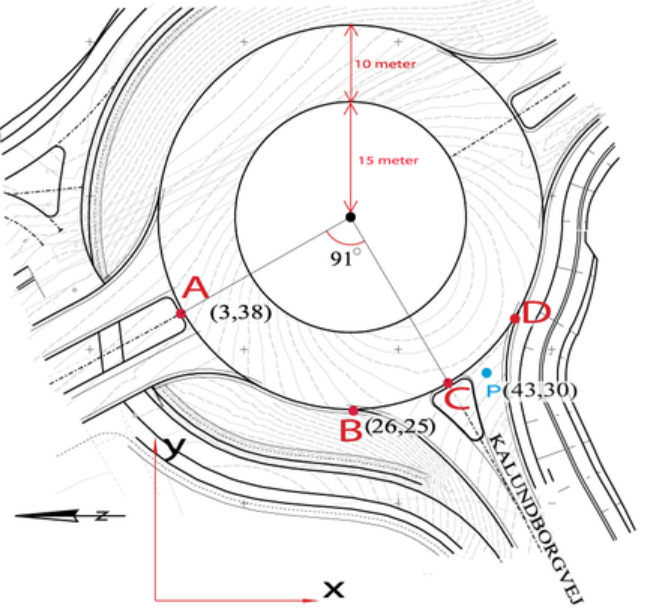
den handler om Rundkørslen : Der gøres opmærksom på at Koordinatsystemet anbringes i rundkørslens midte
1) Hvor lang tid vil det tage at køre en hel tur midt i rundkørslen med en anbefalet max hastighed på 30 km/t?
") Bestem koordinaterne til punkterne C og D, når det gives, at Kalundborgvej møder rundkørslen symmetrisk fra B til D. Vinklen imellem de to veje er 91 grader. Bestem herefter vinklen imellem de to tangenter til cirklen i punkterne A og C samt B og D.
Figur vedhæftes .
Tak på forhånd.
Svar #1
10. juli 2020 af StoreNord
spl 1
Hvis rundkørslen ikke er 2-sporet, skal du vel køre rundt i en cirkel med radius=20 meter.
Men den er måske netop 2-sporet?
Svar #3
10. juli 2020 af Eksperimentalfysikeren
Regn A og B om til polære koordinater. Alle fire punkter har samme modulus, da de ligger på samme cirkelperiferi. Argumenterne for C og D finder du så ved at regne på vinklerne. Regn derefter C og D om til retvinklede koordinater.
Brug de vinkler, du har fundet til at finde vinklerne mellem tangenterne.
Svar #5
10. juli 2020 af DeepOcean
Opgaven skal løses ved brug kun Analytisk planegeometri og ikke andre emne fx vektor polær form.!
# 1 Det er 2- sporet
#3 Du mener med polær form at A = 38,11 vinkel 91 , hvis det er det du mener så har vi brugt vektor viden det må vi ikke !
Stadigvæk jeg savner lidt meget konkret løsning forslag indenfor Plangeoemetri , hvis nogle det har en god ide?
Svar #6
10. juli 2020 af HF2dk
#5Opgaven skal løses ved brug kun Analytisk planegeometri og ikke andre emne fx vektor polær form.!
# 1 Det er 2- sporet
#3 Du mener med polær form at A = 38,11 vinkel 91 , hvis det er det du mener så har vi brugt vektor viden det må vi ikke !
Stadigvæk jeg savner lidt meget konkret løsning forslag indenfor Plangeoemetri , hvis nogle det har en god ide?
Hvor meget mangler du ?
Svar #7
10. juli 2020 af HF2dk
Opgave 1: Bliver i nødt til at bestemme omkredsen af cirklen hvor turen finder sted. Det er lig radius af den inderste cirkel plus halvdelen af forskellen mellem disse.
10/2+15=20
20*2=40
Så kan i bestemme omkredsen af cikrlen
40*pi=125,66 meter
Nu kan man så finde tiden det vil tage køre en omgang
afstand/hastighed=tid
Da afstanden skal være samme enhed hastigheden, så omregner i fra meter til klimeter
125,66/1000=0,12566 kilometer
Så vil ligningen således se sådan ud:
tid=0,12566km/30km/t=0,004189 timer
Dette kan man så omregne til sekunder
0,004189*60*60=15,0793 sekunder
Hjælper kun på denne måde i anledning. Fordi der er sommerferie.
Svar #9
10. juli 2020 af DeepOcean
#8 Tak for det nu er der først del af opgave er på plads .
Måske skal vi kigge på hvordan vi kan bestemme koordinator til Punkt C og D ? hvis andre har lidt tid? / god ide?
Svar #10
10. juli 2020 af HF2dk
Metode til løser næste del er først, skal i bestemme hældning af linjen går gennem punktet A og midtpunktet
a=y2-y1/x2-x1
49,98-38/24,94-3=0,54604
Dette kan i så benytte tan^-1 for at finde vinklen mellem linjen L og den linje går gennem punktet A og midtpunktet
tan^-1(0,54604)=28,64 grader
Så kan i finde hældningen af linjen går igennem punktet C og midtpunktet.
tan(90+28,64-180)=-1,76
Nu vælger i så sætte hældningen ind i formlen, som jeg anvendte før og derefter bruger cirklens lining med 2 ubekendte
-1,76=49,98-y/24,94-x
og
25^2=(x-24,94)^2+(y-49,98)^2
Så indsætter Maple
solve(-1,76=49,98-y/24,94-x og 25^2=(x-24,94)^2+(y-49,98)^2
Dermed får i et resultat hedder
Svar #11
10. juli 2020 af ringstedLC
2) OA, OC og de to tangenter i A og C danner en firkant med to rette vinkler og én kendt.
#0Der gøres opmærksom på at Koordinatsystemet anbringes i rundkørslens midte
Det passer jo ikke med figuren.
Svar #12
10. juli 2020 af HF2dk
#112) OA, OC og de to tangenter i A og C danner en firkant med to rette vinkler og én kendt.
#0Der gøres opmærksom på at Koordinatsystemet anbringes i rundkørslens midte
Det passer jo ikke med figuren.
Har lagt mærke til det, min fejl
Svar #13
10. juli 2020 af StoreNord
Er der ikke en "Analytisk metode" til at dreje et punkt 91 grader?
Svar #15
10. juli 2020 af DeepOcean
#12 så kan man ikke løse opgave hvid koordinatsystem anbringes i rundkørslen? eller måske har jeg misforstået det?
Svar #16
10. juli 2020 af StoreNord
At indlægge et andet koordinatsystem er noget man bruger til at dreje et punkt som A en bestemt vinkel. Her skulle det så være 91 grader, men Jeg kan ikke finde en opskrift på anden vinkel end 90 eller 270 grader.
Har du kunnet bestemme centrum eksakt?
Svar #17
10. juli 2020 af DeepOcean
Måske vil der hjælpe hvis jeg tilføje de to spørgsmål til opgave som blev stillet før de forrige spørgsmål :
A) Bestem cirklens ligning for vejbanens inderste cirkel, hvis koordinatsystemet anbringes i rundkørslens midte.
B) Bestem cirklens ligning for den yderste cirkel, der går igennem punkterne A (3,38) og B (26,25) i det indlagte koordinatsystem
Det er nem t man løse disse spørgsmål men speical ved B) kunne man ikke bruge den ligningen til bestemme Punkt B og D ??
Svar #19
10. juli 2020 af HF2dk
B:
radius er 25, da radius i den inderste cirkel er 15, og radius i den yderste er 10.
Punkt a
(3 − a) 2 + (38 − b) 2 = 25^2
Punkt b
(26 − a) 2 + (25 − b) 2 = 25^2
Så nu benytter jeg substitutionsmetoden til at isolere x og y i en af ligningerne.
((3 − a) 2 + (38 − b) 2 = 25^2 and (26 − ??) 2 + (25 − ??) 2 = 25^2
Svar #20
11. juli 2020 af ringstedLC
Med cirklens ligning har du eksakte værdier for centrum O.
- Konstruer/beregn OB.
- Konstruer/beregn vinkel BOC som differensen mellem 91º og vinkel AOB.
- Konstruer/beregn OD. Benyt symmetrien omkring C.
NB (til næste gang): Upload et billede af hele opgaven, skriv hvad du skal have hjælp til at finde ud af, upload evt. dine egne forsøg på beregninger. Sidst, men ikke mindst, svar på de spørgsmål som hjælperne stiller, ex i #16.