Matematik

Integralregning - Areal under kurven

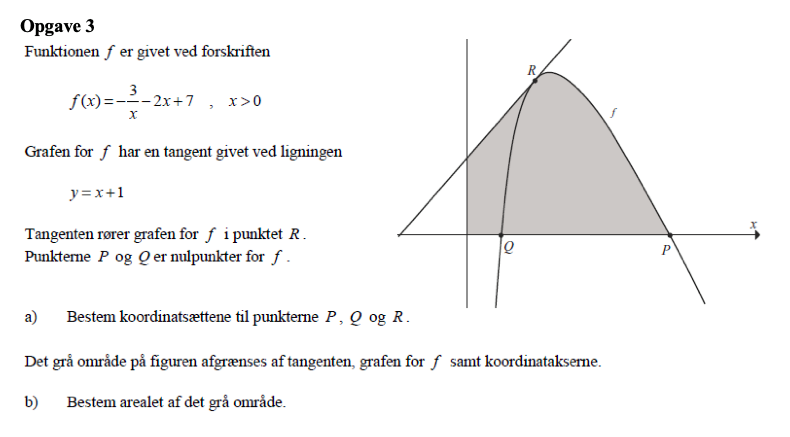
08. december 2020 af marielinge - Niveau: B-niveau

Hvordan løses b?

Prøvede at bestemme arealet under kurven mellem to kurver. Dette gav mig dog et infinity tegn som svar.

Skal jeg opdele arealet i 3?

Så fra origo til punkt R skal arealet bestemmes under kurven for tangenten y, så vi får Areal 1

Så fra punkt Q til R skal arealet bestemmes under kurven for parablen y, så vi får Areal 2

Så fra punkt Q til P skal arealet bestemmes under kruven for parablen f(x), så vi får Areal 3

Atotal = A1 + A3 - A2

Er dette korrekt?

Vedhæftet fil: Skærmbillede 2020-12-08 kl. 10.43.11.png

Brugbart svar (0)

Svar #1
08. december 2020 af peter lind

Brugbart svar (0)

Svar #2
08. december 2020 af PeterValberg

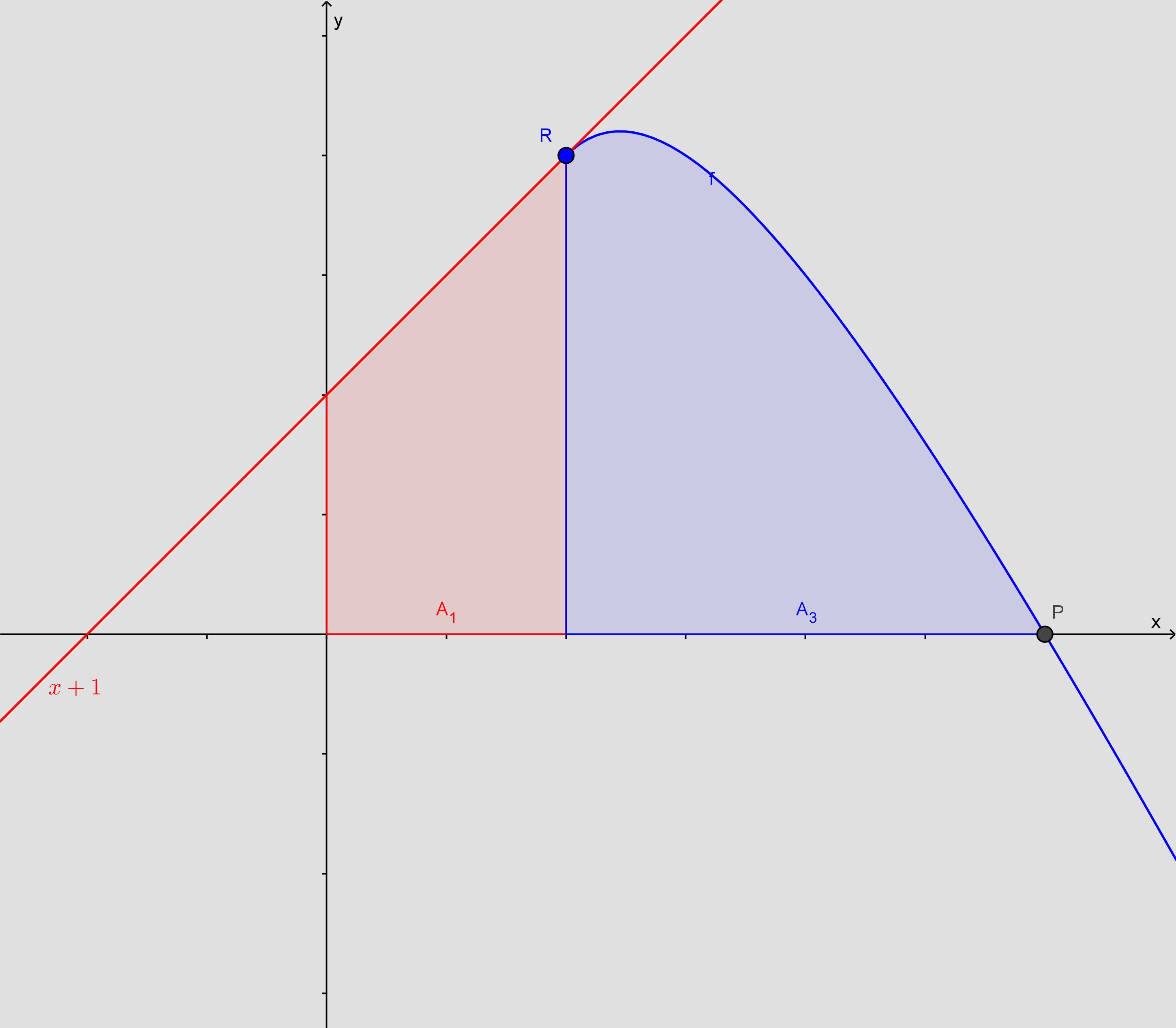
~~Jeg indsætter lige dit vedhæftede billede, det gør det lidt nemmere at hjælpe~~

Den anden Peter var hurtigere end mig :-)

- - -

mvh.

Peter Valberg
(YouTube)

Brugbart svar (0)

Svar #3
08. december 2020 af peter lind

Du skal kun lave det som summen af to arealer nemlig det du kalder A1 og A3

Svar #4
08. december 2020 af marielinge

Men kan det garanteres at A1 er god nok, altså at den tager arealet mellem y(x) og parablen?

Tænker nemlig da at jeg har sat den øvre grænse ved R, så går ned fra R og ned mod x-aksen, og der skærer den igennem parablen. Derfor tænker jeg om man måske skal subtrahere mellem R og Q?

Brugbart svar (0)

Svar #5
08. december 2020 af peter lind

Det du beregner med A1 er arealet af en trapez. Du får altså også arealet under parablen med. Har jeg misforstået hvad du med A1?. Under alle omstændigheder er det nemmeste at beregne trapezens areal. Det kan gøres ved at integrere tangentens ligning fra 0 til x koordinaten for R eller rent geometrisk

Svar #6
08. december 2020 af marielinge

Så jeg skal bestemme arealet fra origo til R med y(x) og fra R til P med f(x)

Så jeg skal slet ikke bruge Q til noget?

Brugbart svar (0)

Svar #7
08. december 2020 af peter lind

Du skal bruge x koordinaten til Q

Svar #8
08. december 2020 af marielinge

Ej du må lige skære det ud i pap for mig - er blevet helt forvirret over hvordan jeg skal gøre det og hcilke punkter jeg skal benytte..

Brugbart svar (0)

Svar #9
08. december 2020 af peter lind

∫₀^t x+1dx hvor t er x koordinaten til Q

Svar #10
08. december 2020 af marielinge

Det vil sige:

A_Total = ∫₀^t1 x+1dx + ∫_t1^t2 x+1

Hvor t1 = x-koordinat til Q

Hvor t2 = x-koordinat til P

Brugbart svar (0)

Svar #11
08. december 2020 af mathon

$\small \small \small \begin{array}{llllll}b)\\& A=\int_{0}^{1}(x+1)\,\mathrm{d}x+\int_{1}^{3}\left ( -\frac{3}{x}-2x+7 \right )\mathrm{d}x \end{array}$

Brugbart svar (0)

Svar #12
08. december 2020 af ringstedLC

Vedhæftet fil:__0.png

Skriv et svar til: Integralregning - Areal under kurven

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.